Introduction of Magnetic Dipole, dipole moment and Bar magnets
The discovery of magnetism is credited to a Greece shepherd named Magness, who lived in Magnesia, Greece. This discovery was accidental while he was herding his sheep through the mountains. He eventually noticed that the funeral of his stick and nails in his sandals stuck to a rock. Because of the attraction of the funeral of his stick and nails in his sandals by the rock, his town was named magnetite after the name of this effort, or the country it was found in.
It was also known as a lodestone because of its attractive properties. Magnetite is one of the three naturally occurring oxides of iron. William Gilbert was an English Scientist (1544-1603) who mentioned techniques of artificially making magnets from steel and was called the father of electricity and magnetism. Sir Oersted studied deeply how electric currents and magnetism are empirically related and discovered the magnetic effect of current. However, enough information regarding the phenomenon of magnetism and some of the basic properties of magnetism were known since 1800.
Bar Magnet and its Properties
Magnetism is the phenomenon of attracting some materials like iron, cobalt, nickel etc. An object that attracts these magnetic materials towards it, is called as a magnet. If this attracting body is of the shape of a bar, then it is called a Bar magnet. Some important types shapes of the magnets are shown in the Fig. -1, here

When a bar magnet is immersed in an iron powder and is then taken out, we observe that the iron powder clings to it, not uniformly but heap up at the end of the bar magnet and thinly over the rest of its body as shown here.
The points in a bar magnet where the iron powder heaps up are called magnetic poles. Thus, the magnetic poles are defined as region in a magnet where the magnetic attracting force is maximum as shown in Fig. 2

Properties
- 1. Directive Property: When a bar magnet is suspended freely to a rigid support with a unspun thread, it aligns itself almost parallel to the direction of earth’s magnetic field and hence along geographical N-S line, in such a way that the north pole of the magnet is in the direction of the north of the earth and S- pole of the magnet points in the direction of the geographical south of the earth as shown in Fig. 3

2. Attractive Property: A magnet possesses the property of attracting the small pieces of magnetic materials like, Iron, cobalt, nickel, and steel towards itself and it is not uniform throughout the entire length of the magnet but is maximum at the poles. The magnetic poles are not situated exactly at surface of the ends but slightly inward into the body as shown in Fig. 3
4. Magnetic poles exist in pairs: When a magnet is cut into two pieces, we see that each piece will act as the independent magnets each having two poles. If we go on dividing this way, each piece will behave like an independent magnet.
If a magnet is cut into two equal pieces along the length of the magnet, then each piece will act as the magnet having pole strength exactly half of the pole strength of the original magnet.
Thus, it is to conclude that in magnetism, mono pole never exists in contrary to that in electricity where an isolated charge exists as shown in Fig. 7
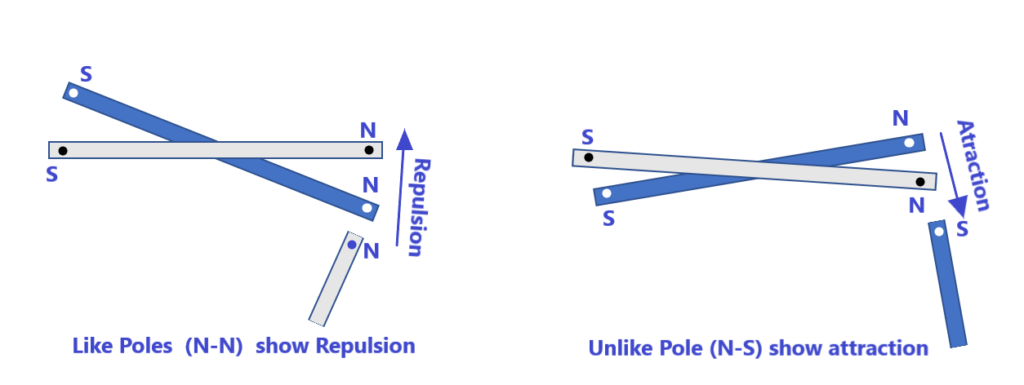
3. Like poles repel and unlike poles Attract: When the N – pole of one magnet is brought near the N-pole of the other magnet, we see they repel each other. Similarly, a S-pole of one magnet repel the S-pole of the other magnet. But on the other hand, a S-pole of one attract the N-pole of the other and vice versa. Therefore, as is seen form the fig. Like pole repel and Unlike pole attract each other as shown in Fig. 5

5. Inductive Property: When a specimen of any magnetic material like iron, cobalt, nickel, and steel is brought near and in the vicinity of a permanent magnet, then we observe that this specimen starts behaving like a magnet itself. The magnetism so acquired by a specimen is called an induced magnetism and the property of a magnet to induce the magnetism is called inductive property.
6. Repulsion is the sure test for testing a magnet: Let us suppose that two identical bars A and B, of which one is simply a bar of iron and the other is the magnet. In order to identify, which of the two is magnet and the other is a metal bar, we bring a magnet near both the ends of bar A and see the result. If it is attracted for its both ends near the magnet, then it is not a magnet but a piece of iron. Now we bring another identical bar B with its both ends near the magnet turn by turn, we see that for one end near the magnet it will be attracted but for the other end towards the magnet it will be repelled showing that it is a magnet. Therefore, repulsion is the sure test to differentiate a magnet from the identical piece of iron metal
Explanation of Magnetism in terms of atomic Theory
We know that the electrons in the atoms revolve in their orbits with so high speed that their orbits are considered to be a current loop. According to Ewing, each molecule in a magnetic material act as a magnetic dipole (tiny magnet) having certain dipole moment. In unmagnetized magnetic material, the magnetic moment of the molecules are randomly distributed (shown by arrows in fig. 8) in all possible directions giving rise to no net magnetic moment. Therefore, the specimen of magnetic materials do not exhibit magnetism
But contrarily, in case of bar magnets the magnetic moment of these tiny molecular magnets are perfectly aligned in same direction such that their N-poles point in same direction and S-poles also point in same and opposite direction to that of N-poles. This results into the fact that one end of the specimen becomes a N-pole while the other becomes S-pole. For a material to be a magnetized or not magnetized depends upon the fact that the distribution of the magnetic moment of all the molecular magnets in it, is aligned in one direction or is randomly distributed.

But contrarily, in case of bar magnets the magnetic moment of these tiny molecular magnets are perfectly aligned in same direction such that their N-poles point in same direction and S-poles also point in same and opposite direction to that of N-poles. This results into the fact that one end of the specimen becomes a N-pole while the other becomes S-pole. For a material to be a magnetized or not magnetized depends upon the fact that the distribution of the magnetic moment of all the molecular magnets in it, is aligned in one direction or is randomly distributed as shown in Fig. 9

Conclusion is drawn here that Ampere, a pioneer in the field of electric current who put forward the theory of elementary atomic magnets in the magnetic substances were electron orbits as considered to be the current loops seems to be true in principle. The atomic magnetism is of electric origin. It is to be pointed here, that the spin motion of the electrons is also the contributor of the magnetism rather than their orbital motion only.
Coulomb’s Law in Magnetism
Statement: There exists a force of attraction or repulsion between the two magnetic poles of strength m1 and m2 separated through a distance d is

Thus, the magnetic pole strength of a magnetic pole is said to be 1 Ampere- meter, when it attracts another unlike pole of same pole strength with a force of 10-7 N placed in vacuum at a distance of 1 meter from it.
Or
Thus, the magnetic pole strength of a magnetic pole is said to be 1 Ampere- meter, when it repels another equal and similar pole of same pole strength with a force of 10-7 N placed in vacuum at a distance of 1 meter from it.
Magnetic dipole and magnetic dipole moment
Magnetic dipole:
Magnetic dipole is a system that consists of two magnetic poles of equal strength and of opposite nature situated at some finite distance. Since a bar magnet has two poles, N-pole and S- pole, both are of equal pole strength, say m, and separated by a finite distance and are of opposite nature, therefore it is called as a magnetic dipole.
The two poles of the magnetic dipole are situated slightly inward into the body rather to be situated at the surface of the ends of the bar magnet. Thus, the distance between the poles of the bar magnet is called as the magnetic length which is always less than the geometrical length of the bar magnet. The magnetic length is a vector quantity directed from S-pole to N-pole of the magnet and the magnitude is 2l

Magnetic Dipole Moment:
The strength of a magnetic dipole is expressed in terms of a physical quantity called as Magnetic Dipole Moment whose magnitude is represented by the product of the strength of either pole and the length of the magnet M = m (2L) and the direction is from S-pole to N-pole of the magnet



Current loop as a magnetic dipole
Let us suppose that an electric current I passes through a circular coil of radius r in the anticlockwise direction in top view. The magnetic lines of induction will form the closed and circular path for each elementary portion of the current loop except at the center of the current loop where it is a straight line. The direction of the magnetic field lines is found applying right hand thumb rule which shows that the field lines appear to enter at the lower face of the coil and exit at its upper face.
This gives a conclusion that the lower face of the coil where the field lines enter behaves as the S- pole while the upper face where the field lines exit the coil behaves as the N-pole. Thus, the coil carrying electric current / current loop behave like a magnetic dipole whose magnetic moment M depends upon the following factors.
- 1. Magnetic moment is directly proportional to the electric current passing through the coil, and
- 2. Magnetic moment is directly proportional to the area of current carrying coil, So



We can also write the above equation as
M = n I A
The term n I in above eq. is called as ampere turns circular coil carrying current, therefore, the magnetic dipole moment of the circular coil carrying current is equal to the product of ampere turns and area of the coil.
Atom as a magnetic dipole and expression of Atomic Dipole Moment
The electrons, in an atom revolve round the nucleus in circular orbits with a so high speed that their orbits are considered as the current loops, each is associated with magnetic moment. The vector sum of the magnetic moment of the current loops due to all electrons in an atom gives it’s a net magnetic moment. Therefore, an atom behaves like a magnetic dipole as it has the magnetic moment.
Expression of Magnetic Dipole Moment of an electron in the orbits
Let us suppose that an electron of mass m and charge e is rotating in a circular orbit of radius r around the nucleus in an atom in anticlockwise direction. If v is the speed of the electron in this orbit, then the angular momentum of the electron due to its orbital motion will be directed normal to the plane of the orbit and in upward direction as shown in fig. 13 below whose magnitude L can be written as L = mv r




As is evident that an electron possesses orbital as well as spin motion in an orbit and both the motion contribute to the total magnetic dipole moment but Eqn. 11 is only due to orbital motion only.
Magnetic Field and its expression at any point on the Axial Line and Equatorial Line of a bar magnet
Magnetic Field
The magnetic field is defined as a region around its source (a magnet/ a current-carrying conductor) in which force is experienced by a magnetic pole when placed at any point. A magnetic field is geometrically represented by a set of lines with the arrows put on one end of each line as shown in the fig. given below

The magnetic is said to be a uniform field if its direction as well as the magnitude remain same at all the points inside it is represented by a set of equispaced parallel lines with the arrows point in same direction while the non-uniform magnetic field is represented by a set of non-equispaced parallel lines with the arrows point in the direction as shown in the fig. above. The SI units of magnetic field induction is Tesla. such that one 1 Tesla ( T ) = 1 newton. ampere-1 meter-1 ( 1 N A-1 m-1 ) . Magnetic flux density / magnetic field induction is also measured in Gauss such that 1 Gauss = 10-4 Tesla ( T )
Magnetic Field at any point on the Axial Line of a bar magnet
Let us suppose that K is a point on the axis of a bar magnet of magnetic length 2l, strength of each pole is m, at a distance r from its mid-point O where the magnetic field is to be found as shown in fig. below

Now we calculate the magnetic fields at point K due to N-pole and S-pole of magnet separately and the vector sum of these fields will give us the magnetic field at point K due to the bar magnet on its axial line . The magnitude of the magnetic field at point K at a distance r from the midpoint O of the bar magnet on its axis due to the N-pole is will be


Magnetic Field at any point on the equatorial line of a bar magnet
Let us suppose that K is a point on the equatorial line of a bar magnet of magnetic length 2l, strength of each pole is m, at a distance r from its mid-point O where the magnetic field is to be found as shown in fig. below

Now we calculate the magnetic fields at point K due to the N-pole and S-pole of the magnet separately and the vector sum of these fields will give us the magnetic field at point K due to the bar magnet on its equatorial line. The magnitude of the magnetic field at point K at a distance r from the midpoint O of the bar magnet on its equatorial line due to the N-pole and S-pole will be


Torque on a Bar Magnet when placed in a magnetic field.
Consider that a bar magnet of magnetic length 2l is placed in a uniform magnetic field B at an angle theta with the direction of magnetic field. Each pole of the bar magnet of pole strength m will experience force as shown in the fig. given below.

The force experienced by N-pole of the bar magnet F = m B in the direction of magnetic field and that by S-pole F = m B in the direction opposite to the direction of magnetic field. We see from the figure above that the forces experienced by the poles are
- Equal in magnitude ( the force experienced by each pole is F = m B )
- Opposite in direction, and
- have different lines of action
Such type of forces possessing the three characteristics make a couple. The tendency of this torque is to rotate the magnet in the clockwise direction. The moment of this couple that is called as a Torque. The magnitude of this torque is given by the product of either force and the perpendicular distance between their lines of action. Thus we can write

Units of magnetic dipole moment

Potential Energy of a bar magnet placed in a magnetic field
Consider that a bar magnet of magnetic length 2l and magnetic dipole moment M is placed in a uniform magnetic field B making an angle theta with the direction of magnetic field. The magnetic dipole under this position will experience a torque whose magnitude is given by




Gauss’s Law in magnetism
Gauss’s Law in magnetism is one of the most important formulation in Maxwell’s electromagnetic theory. Gauss’s Law in magnetism is understood and studied in conjunction with the Gauss’s Law in electrostatics which states that the surface integral of the normal component of electric field taken over a closed surface S is one over epsilon zero times the total net charge enclose within the surface, thus

The existence of an isolated charge in electrostatics is affirmed here in eqn. 29 but the existence of mono pole in magnetism is totally ruled out but there exists a pair of two poles each of equal strength and of unlike nature so, an equation in magnetism identical to the eqn. 29 in electrostatics can be developed as

This eqn. 30 reveals that the surface integral of the normal component of magnetic field taken over a closed surface is always zero. This is called as Gauss’s Law in magnetism that is having the following direct consequences
- An isolated magnetic pole never exists rather magnetic poles always occur in pairs, meaning that the two poles, one N-pole and the other S-pole of equal pole strength forms the pair to exist.
- Whatever the magnetic lines of induction enter a closed surface, the same in number will leave that closed surface.
Magnetic lines of force of magnetic dipole and their properties
The magnetic lines of force also called as magnetic lines of induction or magnetic field lines are considered to be the path along which an isolated north pole tends to move, if it is let free to move. The significance of the magnetic field lines lies in the fact that they are used to visualize the field in terms of strength. The magnetic field is considered to strong in the region where the lines of induction are closely spaced and weaker where the field lines are widely spaced as shown in the fig. below

Properties of Magnetic Lines of Force
- The magnetic lines of force form the closed and continuous loop having neither the starting nor the termination points. The lines are directed from N-pole to S-pole out side the magnet and from S-pole to N-pole with in the body of the magnet as shown here

2. The direction of the magnetic field at any point is represented by the tangent drawn on the field line at that point, as shown in the fig. above

3. No two magnetic lines of induction intersect each other at any point. If the two lines intersect at some common point say at P. Then at the point of intersection P, the two tangents are drawn showing the two directions of the field at point P. This not possible as field can never have dual direction at a single point. Thus. no two lines can intersect at a single point.




2 Comments