Mirror Formula -12
It is the relation between the distance of the object(u), the distance of the image (v), and the focal length of the spherical mirror.
The mirror formula can be derived by making use of different sign conventions. However, We shall drive the mirror formula for a spherical mirror of small aperture by adopting new cartesian sign convention. Therefore, we shall first discuss these new sign conventions before we, derive the mirror equation as follows.
New cartesian sign conventions -Mirror Formula -12
While we study the mirror formula and the images formed by the spherical mirrors, we first discuss new Cartesian sign conventions, which are given as followings.
- 1. All the distances are measured from the pole of the mirror. (Mirror Formula -12)
- 2. The distances measured in the direction of the incident light are taken as positive, while the distance measured in the direction opposite to that of the incident light, are taken as negative. (Mirror Formula -12)
Obviously, the object distance (u), when measured from the pole of the spherical mirror will always be in a direction against the incident light and hence, it will be negative. In case the image is formed in front of the mirror, therefore, on the same side of the object, the image distance (v) will also be negative. Since such an image can be produced on the screen, the image is formed in front of a spherical mirror is real in nature. (Mirror Formula -12)
On the other hand, if the image is formed behind the mirror, the image distance (v) from the pole of the mirror will be in the direction of the incident light and hence, it will be positive. When the image is behind the spherical mirror, it cannot be brought on the screen, and hence the image formed is virtual in nature. (Mirror Formula -12)
From the figure of the ray diagram, it is clear that the triangle A*B*F and KNF are similar, therefore, A*B*/NK = B* Since, the aperture of the given mirror is assumed to be small, therefore, the points N and P are very close to each other so that NF is relaced by PF and NE = AB, thus, we can write the above eqn. as
Further, in the case of a concave spherical mirror, the focus (F) and the center of the curvature (C), are located in front of a mirror, while in the case of a convex spherical mirror, the points F and C lie behind the mirror. (Mirror Formula -12)
Therefore, measurements of the distances of the points Fand C, therefore, focal length and radius of curvature are against the directions of the incident light in the case of a spherical mirror and in the same direction as that of the incident light in the case of a convex spherical mirror. Therefore, the focal length F and the radius of curvature (R) of the concave spherical mirror are taken as negative while those of convex spherical mirrors are taken as positive.
- The heights measured perpendicular to the principal exes in the upward direction, is considered to be positive, while those measured in the downward direction are taken to be negative. (Mirror Formula -12)
For an erect object (the object is situated about the principal axis); the real image is always inverted, while the virtual image is erect. Therefore, when image is formed by a spherical mirror, the size of the real image is taken as negative, while that of virtual image is taken as positive. (Mirror Formula -12)
Derivation of Mirror Formula -12
The mirror formula, also called mirror equation, is a mathematical formulation which provides an information that how the optical terms, in case spherical mirrors (like the distance of the object(u), the distance of the image (v), and the focal length of the spherical mirror) are related with each other.
For Concave Spherical Mirror
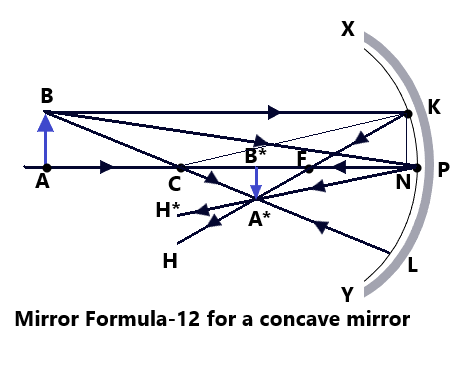
Let us suppose that object AB is placed on the principal axis of a concave spherical mirror at a point beyond the center of curvature C. Let the points P, F, and C be the pole, principal focus, and center of curvature of the concave mirror as shown in the figure of the ray diagram above.
The ray of light from point B of the object travels parallel to the principal axis of the mirror and strikes the mirror at Point K. After reflection, it passes through the focus F of the mirror along KFH.
Another ray of light from point B is incident at the pole P of the mirror, which will be reflected according to the laws of reflection making an angle BPA equal to angle H*PA. Also, the ray of light BL passes through the center of the curvature C and will be reflected back along LB. The raves KH, PH*, and LB meet at point A*. Thus, a real image B*A* is formed of the object. From the point K, drop KN perpendicular to the principal axis.
From the ray diagram, it is clear that the triangle A*B*F and KNF are similar, therefore, A*B*/NK = B*F/NF Since, the aperture of the given mirror is assumed to be small, therefore, the points N and P are very close to each other so that NF is relaced by PF and NE = AB, thus, we can write the above eqn. as


This equation 04 is the relation among the optical quantities like focal length, object distance and image distance for the concave mirror and is called mirror formula. In terms of radius of curvature, object distance and image distance for the concave mirror, the Mirror Formula -12 can be written as (1/u) + (1/v) = 2/R (as f = R/2)
For Convex Spherical Mirror
Let us suppose that object AB is placed on the principal axis of a convex spherical mirror to the R. H. S of its refracting surface. Let the points P, F, and C be the pole, principal focus, and center of curvature of the convex mirror as shown in the figure of the ray diagram above.
The ray of light from point B of the object travels parallel to the principal axis of the mirror and strikes the mirror at Point K. After reflection, it goes along KQ and appears to passes through the focus F of the mirror along FKQ. Another ray of light from point B is incident at the pole P of the mirror, which will be reflected according to the laws of reflection making an angle BPA equal to angle Q*PA.
Also, the ray of light AP will be reflected back along PA and appears as if it is coming from the center of curvature C of the mirror. Thus, a virtual image B*A* is formed of the object AB on the other side of the mirror. Draw KN perpendicular to the principal axis.


This equation 04 is the relation among the optical quantities like focal length, object distance and image distance for the concave mirror and is called mirror formula. In terms of radius of curvature, object distance and image distance for the convex mirror, the Mirror Formula -12 can be written as (1/u) + (1/v) = 2/R (as f = R/2)
Linear Magnification by concave mirror– Mirror Formula -12
Linear magnification or simply magnification by a concave mirror is defined as the ratio of the size of the image to the size of the object. It is denoted by m and is expressed as m = Size of the Image/ Size of the Object. m = I/O


Linear Magnification by convex mirror– Mirror Formula -12
Linear magnification or simply magnification by a convex mirror is defined as the ratio of the size of the image to the size of the object


It is observed that the equations of the linear magnification or simply magnification for the concave and the convex spherical mirrors are the same irrespective of of the fact that the image formed by the mirror is real or virtual.
Summary of Mirror Formula -12
(A) The radius of curvature and focal length of a concave spherical mirror is taken as positive.
(B)The radius of curvature and focal length of its convex spherical mirror if taken as negative.
(C) A real object is situated in front of a spherical mirror, and therefore, according to new cartesian sign conventions, the distance of a real object from pole of the mirror is taken as negative.
(D) The real image of an object is formed by a concave spherical mirror in front of the mirror. Therefore, according to new cartesian sign conventions, its distance from the pole of the mirror is also taken as negative.
(E) The virtual image of an object is formed by a concave or convex spherical mirror behind the mirror. Therefore, according to new cartesian sign conventions, its distance from the pole of the mirror is taken as positive.
(F) The real image formed by a concave spherical mirror is inverted and therefore, according to new cartesian sign conventions, its size is taken as positive.
(G) The virtual image formed by a concave or convex spherical mirror is erect and therefore, according to new cartesian sign conventions, its size is taken as negative.
(H) A plane mirror may be considered as a spherical mirror of infinite focal length.
