Microscopes-12 Learn in Fun

Microscopes

These are the optical instruments used for observing the minute objects.

Optics is a field of science that studies the behavior and properties of light, including its interactions with matter and the construction of instruments that use or detect it. It has a wide range of applications, from telescopes to microscopes. Microscopes are one of the most important tools in optics, as they allow us to view objects that are too small to be seen with the naked eye. (Microscopes)

Microscopes have been around us for centuries and have evolved over time to provide better magnification, resolution, and clarity. With advancements in technology, microscopes now come equipped with features like digital imaging and computerized control systems. These features make it easier for scientists to study microscopic organisms or objects in detail and gain valuable insights into their structure and function. (Microscopes)

Types of Microscopes:

Simple Telescopes:

It is simply a convex lens of short focal length used to observe a magnified image of a small object. It is also called a simple microscope or a magnifying glass. (Microscopes)

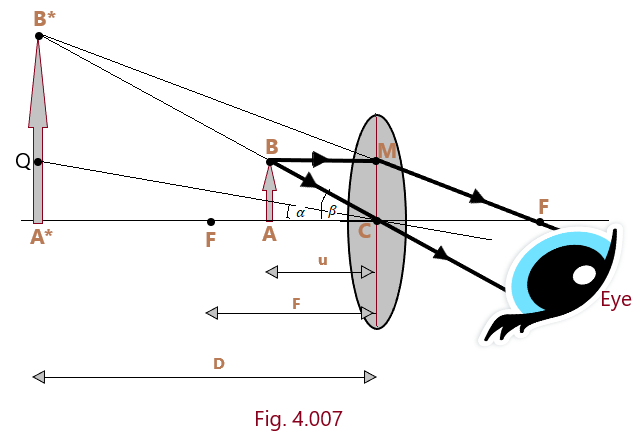
Principle of Simple Microscope:

When a small object is placed between the optical center and the focus of the lens, its virtual, erect, and magnified magnified image is obtained on the same side of the lens. The lens is held close to the eye, and the distance of the object is adjusted till the image is formed at the least distance of distinct vision from the eye. For, a normal and healthy eye, the least distance of descriptivism is 25 cm. (Microscopes)

Working:

Let us suppose that object AB is placed on the principal axis of a convex lens between the focal point F and the center of curvature C. It is observed that its virtual image A*B* of large size is formed on the same side of the object AB. It is also noted that the distance of the image A*B* changes as the distance of the object AB is allowed to change. It is now recommended that the position of the object AB is so adjusted between the points F and C that the image A*B* is formed at a distance equal to the least distance of distinct vision (D) as shown in [Fig.4.007]. (Microscopes)

Magnifying Power (When the image is formed at D)

Magnifying Power of a simple microscope is defined as the ratio of the angle subtended by the image at the eye to the angle subtended by the object when seen directly when both (object and the image) lie at a distance equal to the least distance of distinct vision. This magnifying power of the simple microscope is also called angular magnification and is denoted by M. Thus, by the definition, the magnifying power of the simple microscope is given by

The magnifying power of a simple microscope can also be expressed in different form using f as the focal length of the simple microscope. Thus,

The Eqn. 4.03 represents the another form of magnifying power of the simple microscope. From this expression, the following conclusions can be drawn.

1. Smaller the focal length of the simple microscope, larger will be its magnifying power and vice-versa. (2). The magnifying power of the simple microscope is positive that implies that the image formed is erect and hence virtual.

Magnifying Power (For the image formed at infinity)

Magnifying Power of a simple microscope is defined as the ratio of the angle subtended by the image (situated at infinity) at the eye to the angle subtended by the object at eye, when seen directly when lie at a distance equal to the least distance of distinct vision. This magnifying power of the simple microscope is also called angular magnification and is denoted by M. Thus, by the definition, the magnifying power of the simple microscope is given by

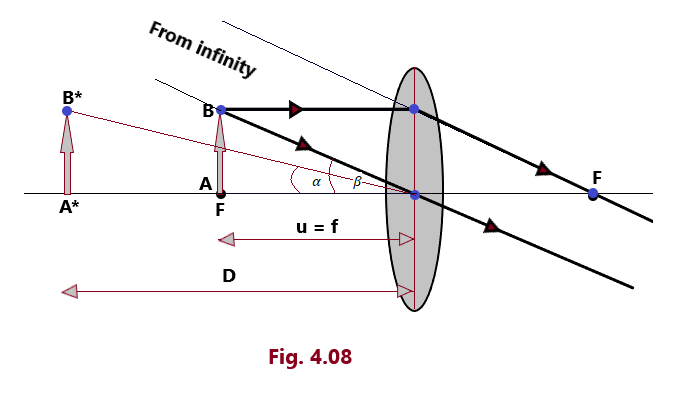
Equation 4.05 gives an expression of the magnifying power of a simple microscope in the case when the image is formed at infinity. In this case, the magnification is less than the magnification when the image is formed at the near point by one. But viewing the magnified image is more comfortable when the image is formed at infinity.

Use of Simple Microscope:

• Jewelers and watch makers generally make best utilization of the convex lens of short focal length as a simple microscope to see the magnified view the fine jewelry work and the magnified view of the tiny parts of the watches.
• Magnifying glass is used in science laboratories by the students for reading vernier scales.
• Simple microscopes are used by the dermatologists to see and find out various skin diseases during the primary skin examinations.
• It is used in microbiology labs by the microbiologists to study the samples of algae and fungi etc.

Compound Microscope

A compound microscope is used to observe objects of extremely small size, particularly when simple microscope ceases to stop working efficiently and precisely.

Construction:

Compound microscope consists of two lenses: (1) Objective Lens: It is a convex lens of small aperture and small focal length and it faces towards the object during the course of its function. (2) Eye Lens: It is the lens of moderate focal length and large aperture. These two lenses are mounted coaxially at the ends of two metallic tubes which are capable of moving in and out with the help of reck and pinion arrangements. In order to focus an object, the distance of the objective lens from the object is adjusted with the help of this reck and pinion arrangement. A good quality of compound microscope can produce the magnification in the order of 1000. (Microscopes)

Principle:

When a small object is placed just outside the focus (F₀) of the objective lens its real, inverted and magnified image is formed on the other side of the lens beyond (F₀). The image produced by the objective lens acts as object for the eye lens. The distance of the object from the objective lens is so adjusted that the final image is formed at the least distance of distinct vision from the eye. (Microscopes)

Working:

Let us consider that an object AB is placed on the principal axis of the objective lens just beyond its principal focus F₀ so that its real, magnified and inverted image A*B* is formed on the other side of the objective lens between the focal point F_e and optical center C* of the eye lens as shown in [Fig. 4.09]. (Microscopes)

The A*B* formed by the objective lens of an object AB acts as an object for the eye lens. Now with the help of reck and pinion arrangement, the distance between the object lens and the object AB is so adjusted that its virtual and magnified image A**B**is formed by the eye lens on the same side at a distance equal to the least distance of distinct vision.  

Magnifying Power:

Magnifying power or angular Magnification of a compound microscope is defined as the ratio of the angle subtended by the final virtual image at the eye to the angle subtended by the object at the eye when the both are assumed to be placed at a distance equal to the least distance of distinct vision. (Microscopes)

Determination of Magnifying Power: Let us suppose that the angle A**C*B** is the angle that the final image subtends at the eye and the angle B**C*Q is the angle that the object subtends at the eye when both are supposed to lie at a distance equal to the least distance of distinct vision and if these angles are quite small angles, then the magnifying power can be written as

Magnifying Power when the final image is formed at infinity:

The magnifying power of a compound microscope when the final image is formed at infinity is defined as the ratio of the angle subtended at the eye by the final image formed at infinity to the angle subtended at the eye by the object when seen directly.

The final image due to a compound microscope is formed at infinity when the image A*B* formed by the objective lens lies at the focal point F_e of the eye lens. It implies that u_e = f_e in the case the final image A**B** is formed at infinity. The magnifying power of the objective lens will be m₀ = v_o / (-u_e) = L/(-f_o) and the magnifying power of the eye lens when the final image is formed at infinity, m_e = D / f_e Therefore, the magnifying power of the compound microscope will take the form m = m_o x m_e = v_o / (-u_e) x D / f_e = L/(-f_o) x D / f_e

L= v_o + u_e is the length of the microscope which said to be in normal adjustment. The magnifying power of the compound microscope will be larger for smaller values of the focal lengths of both objective lens and eye lens f_o and f_e (Microscopes)

Inferences

• A crosswire can be used as the intermediate image is formed between the two lenses, objective lens and eye lens.
• The defects of the images, specially spherical aberration is minimized because of the reason that the aperture of both the lenses used in the microscope is small. (Microscopes)
• The image viewed in the microscope is always inverted with respect to the object as the magnifying power (m) is negative. By inverted image we mean that upside down and left turned to right. (Microscopes)
• Objective lens and Eye lens, both are formed as a combination of a number of lenses in order to increase the quality of the compound microscope. In doing so, different types of defects of the image formed by a single lens are minimized. (Microscopes)
• By illuminating the object and by using an oil immersion objective lens, the visibility and quality of the image can be improved to greater extent.
• The field of view of the compound microscope can be increased by taking the eye lens of the focal length f_e larger than the focal length of the objective lens.