Rutherford’s Atom model-12 learn in fun

Rutherford’s Atom model

It furnishes an important insight into the structure of an atom in congruence with some practical observations.

Rutherford’s alpha Particles Scattering Experiment

As an attempt to investigate the structure of the atom, Rutherford along with his two associates Geiger and Marsden studied the scattering of the alpha particles from a thin gold foil. An alpha particle is a positively charged particle having a mass equal to that of helium atom and the positive charge in magnitude equal to twice the charge of an electron and symbolically represented as a helium nucleus He4 They are found to be emitted by many radioactive elements. The alpha particle scattering experiment provided very useful information about the structure of the atom and is the basis of Rutherford’s Atom model. (Rutherford’s Atom model)

Experimental setup:

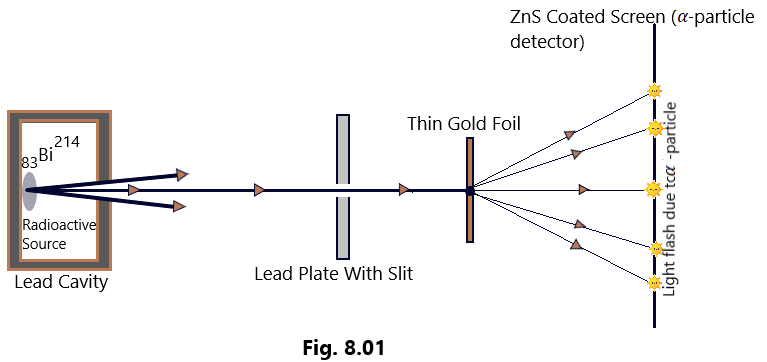
Experimental setup: The Alpha particles from Bismuth (₈₃Bi²¹⁴), a radioactive source, contained in a lead cavity, are collimated into a narrow beam with the help of a lead plate having a narrow slit as shown in [Figure 8.01]. The narrow beam of alpha particles then falls on a thin gold foil about 2.1 x 10^-10 m thick. The alpha particles scattered in different directions were detected with the help of an alpha particle detector. The whole apparatus was arranged inside a vacuum chamber to prevent the scattering of alpha particle from air molecules. (Rutherford’s Atom model)

Observations: The following observations were made about the scattering of alpha particles from a gold foil.

1. Most of the alpha particles were found to pass through the gold foil without any appreciable deflection. (Rutherford’s Atom model)
2. In passing through the gold foil, the different alpha particles underwent different amounts of deflections. (Rutherford’s Atom model)
3. A very small number of Alpha particles (about 1 in 10,000) practically retraced their paths or suffered a deflection of nearly 180^o. (Rutherford’s Atom model)
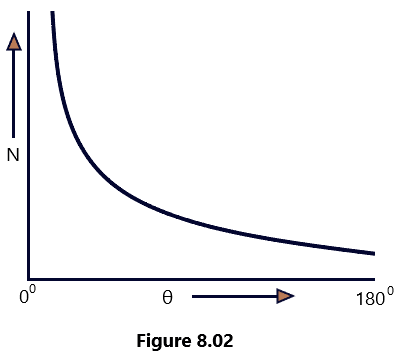
4. The graph between the total number of alpha Particles N(θ) scattered through an angle θ and the scattering angle θ was found to be a shown in [Figure 8. 02]. (Rutherford’s Atom model)

       The alpha particles scattered from the gold    foils are very heavy particles (about 7000 times heavier than the electrons) and possess high initial speeds. Thomson’s atom model cannot explain the scattering of alpha particles through large angles and particularly through 180 degrees. It is because the light particles like electrons cannot deflect the massive alpha particles through 180 degrees. (Rutherford’s Atom model)

Explanation: To explain the above experimental observations, Rutherford assumed that the scattering of alpha particles from the gold atoms was due to Coulomb’s interaction between the positive charge of the alpha particles and the positive charge in the gold atom. On this basis, he theoretically calculated the number of alpha particles that would be deflected through angle θ.  The theoretical graph between N(θ) and θ was found to be in full agreement with the graph shown in the [Figure 8.02] above obtained experimentally. The experimental observation led him to the following conclusions. (Rutherford’s Atom model)

Conclusions:

1. There is an enough empty space with in the atom as it is supported by the fact that most of the alpha particles passed without suffering any deviation. (Rutherford’s Atom model)
2. The scattering of the alpha particles through 180^o, strongly supported the concept of the nucleus. The scattering of the fast and positively charged heavy particles (alpha particles) through 180^o is possible with the consideration that the entire positive charge and practically the entire mass of the atom is confined to an extremely small core called as the nucleus. The size of the nucleus is about (1/10,000) th part of the atom since, 1 in about 10,000 alpha particles under goes deflection through180^o. (Rutherford’s Atom model)
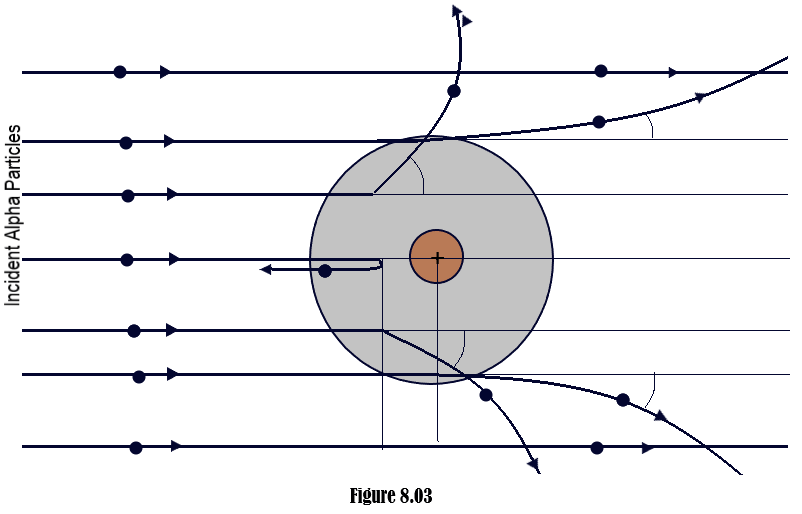
3. The alpha particles which pass through the atom at larger distances from the nucleus, experience smaller electrostatic force of repulsion due to the nucleus and so suffer very small deflection. The alpha  particles which pass through the atom at smaller distances from the nucleus and closer to it, experience larger electrostatic force of repulsion due to the nucleus and so suffer large deflection. The alpha particles which approach the nucleus head on, slow down due to strong electrostatic force of repulsion due to the nucleus, comes ultimately to rest momentarily and then retrace their path after suffering a deflection at 180^oas shown in [Figure 8.03] (Rutherford’s Atom model)

Distance of Closest Approach

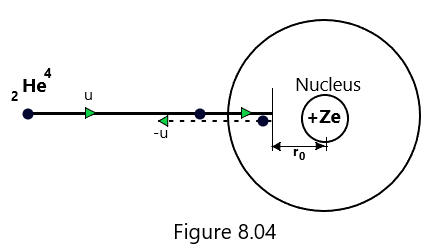
Let us suppose that an alpha particle is travelling towards the atom of the target material and approaches the center of the nucleus head on. It continuously gets slowed down as it approaches the nucleus and at a certain distance, say r₀ from the nucleus, the alpha particle comes to rest momentarily and retraces its path under the deflection of 180^o.  At this moment, its initial kinetic energy is completely converted into electric potential energy. The distance r₀ is called the distance of closed approach, as shown in [Figure 8.04] and its value provides a closer estimate of the size of the nucleus of the target atom.

Let us further suppose that an alpha particle of mass m, when it is at a large distance from the atom, possesses an initial velocity u. At the distance of closest approach, the kinetic energy of the alpha particle is completely converted into potential energy. Mathematically, it is shown that (Rutherford’s Atom model)

The Eqn. (i), given above, represents relation for the distance of closest approach. In the Geiger-Marsden experiment of alpha particle scattering, the alpha particle of kinetic energy 5.5 MeV, were made to incident on the target of thin gold foil (Z= 79). These values when substituted in Eqn. (i), the distance of closest approach r₀ was determined to be 4.13 x 10^-14 m. As its value provides a closer estimate of the size of the nucleus of the target atom, therefore, the size of the nucleus is established to be of the order of 10^-14 m.

This formula provides an approximate estimation and assumes that the alpha particle and target nucleus interact solely through electrostatic forces. t’s important to note that the distance of closest approach will vary depending on the specific experiment, target nucleus, and energy of the alpha particles involved. In Rutherford’s famous gold foil experiment, for example, the distance of closest approach for alpha particles was on the order of a few femtometers (10^-15 m), indicating that the vast majority of the atom is empty space. (Rutherford’s Atom model)

Impact Parameter:

Suppose that an alpha particle (₂He⁴) with velocity u is made to incident on a nucleus of a positive charge +Ze. As shown in [Figure 8.05], when the alpha particle is far from the target nucleus, it moves along a straight line and it scatters along a path making an angle θ with the initial path, on coming closer to the nucleus up to certain distance, called as impact parameter as shown in [Figure 8.05] and is denoted by b.

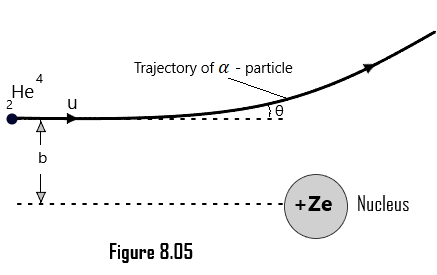
Impact parameter of an alpha particle is defined as the normal distance of the velocity vector of the alpha particle from the center of the nucleus when it is far away from the atom.

The impact parameter greatly affects the scattering of an alpha particle from the nucleus of an atom. The mathematical relation between the impact parameter and the scattering angle was derived by Rutherford and presented as follows

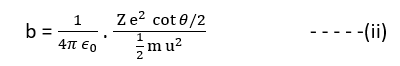
On the discussion, of the expression of the impact parameter given above by equation (ii), the following inferences can be drawn:

1. For the larger value of impact parameter b of an alpha particles, greater will be the value of cot θ/2, implying that the angle of scattering θ is small and vice-versa.

Therefore, the conclusion is that when the alpha particle has large impact parameter, it will get scattered through a very small angle and practically may go undeviated and on the other hand, if the alpha particle has smaller impact parameter, it will get scattered through a large angle.

2. For an impact parameter b = 0, of an alpha particle, then, cot θ/2 =0 ⇒ θ/2 = 90^o ⇒ θ= 180^o

Therefore, when an impact parameter of an alpha particle is zero implying that the alpha particles approach the nucleus directly and head on, it will under goes scattering at 180^o. This is very important to point out that the nature of the trajectory of the scattered alpha particles depends upon the impact parameter in addition to the laws of forces acting between the nucleus and the alpha particles. Thus, it is conclusive to state that the scattering experiment is quite informative to know the nature of force that exists between the nucleus and the scattered particles.

Rutherford’s Atom Model:

Ernest Rutherford, a New Zeeland born Physicist, on the basis of the observations and the results of the experiment in 1909, he conducted along with his associates, Geiger and Marsden, in respect of the scattering of alpha particles incident on a thin gold foil, presented the picture of an atom called as Rutherford’s Atom Model. This atom model is based on the following assumptions:

1. An atom is assumed to be a perfect sphere having a diameter of 10^-10 m. The entire mass of the atom and the whole positive charge be concentrated at the center of the atom in a small spherical region (central core), called as the nucleus having size (diameter) equal to 10^-14 m. It means that the size of the atom is 10,000 times more than the size of the nucleus.
2. The nucleus is surrounded by the electrons called as extra-nuclear electrons which spreads over the remaining part of the atom, leaving plenty of empty space in the atom.
3. The total number of protons with in the nucleus (positive charge of the atom in the nucleus) and the total number of extra-nuclear electrons (negative charge with in the atom) are equal. This is the reason, why an atom is electrically neutral.
4. Rutherford, convinced with the result of his experiment of alpha particle scattering pointe out that the electrons inside the atom are not stationary for if they were at rest, they would be pulled into the positive nucleus due to the strong electrostatic force of attraction between the nucleus and the electrons. He assumed that the electrons are revolving around the nucleus in circular orbits. The necessary centripetal force required for maintaining the circular motion of the electrons is provided to them by the electrostatic force of attraction between the electrons and the nucleus. (Rutherford’s Atom model)

Limitations of Rutherford’s Atom Model:

The Rutherford’s atom model successively explained the shortcomings of Thomson’s Atom Model and provided the explanations to the result of alpha particles scattering as well. Rutherford’s atom model, also known as the planetary model or the nuclear model, was proposed by Ernest Rutherford in 1911. While it represented a significant advancement in understanding atomic structure, it also had several limitations. Here are some of the main limitations of Rutherford’s model:

(1) Electron Stability: Rutherford’s Atom model did not provide an explanation for the stability of electrons in their orbits around the nucleus. According to classical electromagnetic theory, accelerated charged particles should continuously emit energy in the form of radiation and spiral into the nucleus, resulting in the collapse of the atom. However, stable atoms exist in nature, which Rutherford’s model could not account for.

(2) Electron Pathways: Rutherford’s Atom model did not provide a precise description of the pathways followed by the electrons as they orbited the nucleus. It suggested that electrons moved in circular or elliptical orbits, similar to planets around the sun. However, this concept conflicted with the developing understanding of quantum mechanics, which described electrons as having wave-like properties and their locations being described by probability distributions.

(3) Lack of Energy Quantization: Rutherford’s Atom Model did not incorporate the concept of energy quantization. It couldn’t explain why electrons could only occupy certain discrete energy levels and not any arbitrary level. This limitation was addressed by the later development of quantum mechanics.

(4) Neglect of Electron Spin: Rutherford’s Atom model did not account for electron spin, which is an intrinsic property of electrons. Spin plays a crucial role in determining the behavior and properties of electrons, and its incorporation was necessary to provide a more accurate description of atomic structure.

(5) Failure to Explain Spectral Lines: Although Rutherford’s Atom model successfully explained the scattering of alpha particles and the existence of a positively charged nucleus, it could not account for the observed spectral lines in atomic emission and absorption spectra. The model did not provide a mechanism for the discrete energy transitions that lead to the emission or absorption of specific wavelengths of light.

(6) Neglect of Electron-Electron Interactions: Rutherford’s Atom model ignored the electron-electron interactions within the atom. In reality, electrons repel each other due to their negative charges, and these repulsive forces affect the arrangement and behavior of electrons within the atom. The model did not consider these interactions, which are crucial for understanding the stability and structure of multi-electron atoms.

Despite its limitations, Rutherford’s atomic model laid the foundation for subsequent developments in atomic theory and provided the impetus for the development of quantum mechanics, which offered a more comprehensive and accurate description of atomic structure.

Knowledge plus point:

*The alpha particle is about 7,000 heavier than an electron.

*According to the Rutherford’s Atom Model, the mass of an atom is non-uniformly distributed, contrary to that in Thomson’s Atom Model.

*The existence of the nucleus was established by Rutherford’s alpha particle scattering experiment.

*The distance of the closest approach provides the an approximate estimate of the size of the nucleus.

*The kinetic energy of an alpha particle appears as its potential energy, when it is a the distance of the closest approach from the heavy nucleus as a target.

Numerical problems:

Problem 8.01:

In Geiger-Marsden experiment, a 5 M eV alpha particle is scattered through 180^o from a thin gold foil. if the atomic number of gold is 79, find the closest approach to the gold nucleus.

Solution:

Using the relation for the distance of closest approach, we can write,

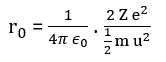
putting the values of all the terms appearing in the above relation, r₀ = 9 x 10⁹ x [(2 x 79 x 1.6 x 10^-19 x 1.6 x 10^-19 )/5 x 1.6 x 10^-13] = 4.55 x 10^-14 m ⇒ r₀ = 4.55 x 10^-14 m

Problem 8.02:

Evaluate the value of impact parameter for the alpha particles scattered through 180^o.

Solution:

Using the relation for the impact parameter, we can write,

putting the values of all the terms appearing in the above relation, we get, b = 0, as for θ=180^o, cot θ/2 = cot 180^o/2 = cot 90^o = 0

MCQs

Q. 01

An alpha particle ₂He⁴ nucleus of energy (1/2) mv² is made to strike a heavy target of charge Ze. Then, the distance of closest approach for the for the alpha nucleus will be proportional to:

Answer:

Q. 02

An alpha particle of energy 5 M eV is scattered through 180^o by a fixed uranium nucleus. The distance of the closest approach is of the order of:

Answer:

Q. 03

Rutherford’s alpha particle scattering experiment shows that the atoms have

Answer:

Q. 04

Rutherford’s alpha particle scattering experiment concludes that:

Answer:

Q. 05

According to the classical theory of Rutherford’s Model, the path of electron will be

Answer: