solids
Solids are a special type of matter in which the structural units, the atoms and the molecules, are very closely packed owing to the existence of strong interatomic and intermolecular attractive forces. This is the reason that solids possess a definite shape and volume. All solids are incompressible and exhibit the properties of rigidity and mechanical strength because they have the property of elasticity. Due to the internal arrangement of atoms and molecules inside them, they have been classified as follows:
Crystalline Solids:
Crystalline solids are those types of solids in which the atoms or molecules are arranged in a definite and regular way throughout the body of the crystal and possess a definite external geometrical shape. Quartz, sugar, mica, copper sulfate, sodium chloride, sugar, etc. are a few examples of crystalline solids.
Characteristics of crystalline solids:
- The arrangement of atoms and molecules in crystalline solids is regular and definite. The crystalline solids, therefore, possess a definite external geometrical shape.
- The crystalline solids possess long-range symmetry in atoms and molecules. This means that the regular and orderly arrangement of atoms and molecules extends over a large volume of the crystal.
- The flat surfaces bound the crystalline solids.
- The physical properties like thermal conductivity, electrical conductivity, compressibility, etc. are different in different directions in the crystalline solids. It means that the crystalline solids have anisotropic properties.
- The chemical bonds between all the atoms, molecules, or ions are of equal strength, leading the crystalline solids to possess uniform chemical composition
- As the chemical bonds between all the atoms, molecules, or ions are of equal strength and they get ruptured at the same temperature when heated. It means that the change from the solid state to the liquid state takes place suddenly, and therefore, crystalline solids are said to have a sharp melting point.
- The crystalline solids are in a stable state below the temperature of crystallization because a stable state is the state of minimum energy. Thus, the crystalline solids acquire a state of minimum energy upon crystallization.
Amorphous solids:
Amorphous materials are solids in which the arrangement of the atoms or molecules is irregular and asymmetrical, so that such types of solids do not have a definite external geometrical shape. Glass, rubber, sulfur, etc. are a few examples of amorphous solids.
Characteristics of amorphous solids:
- The arrangement of atoms and molecules in an amorphous solid is not regular and definite. These types of solids, therefore, do not possess a definite external geometrical shape.
- Amorphous solids possess short-range symmetry in atoms and molecules. This means that the regular and orderly arrangement of atoms and molecules does not extend over a large volume of the solids.
- Physical properties like thermal conductivity, electrical conductivity, compressibility, etc. are similar in different directions in amorphous solids. It means that the amorphous solids are isotropic in character.
- As the chemical bonds between all the atoms, molecules, or ions are not of equal strength, and they do not get ruptured at the same temperature when heated but over a range of temperatures. It means that the change from the solid state to the liquid state takes place over a range of temperatures, and therefore, these solids are said to have a range of melting points.
- The flat surfaces do not bound the amorphous solids.
- The chemical bonds between all the atoms, molecules, or ions are of unequal strength, leading the amorphous solids to possess a non-uniform chemical composition.
Crystal Structure:
Before studying the structure of different types of crystals, the following important terms are to be studied:
Crystal lattice:
The infinite array of atoms and molecules in three-dimensional space, such that at every point, an atom or molecule has the same surroundings, is called the crystal lattice.
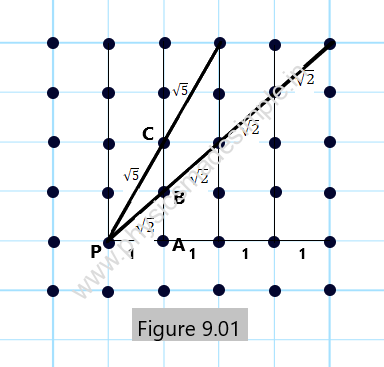
Let us suppose that Figure 9.01 represents a two-dimensional crystal lattice. Let us assume that the interatomic distance along all the coordinates is one unit. Considering an arbitrary point P representing the position of some atom, the distances of the points PA, PB, and PC will be 1 unit, (2)1/2, and (5)1/2, respectively. The same is true for the separation of the points in any other direction when extended infinitely. Therefore, it is fully in accordance with the definition of a crystal lattice in two dimensions.
However, the crystal lattice is three-dimensional, and the arrangement of atoms is very similar to that in the two-dimensional crystal lattice, as shown above in Figure 9.01.
Unit cells:
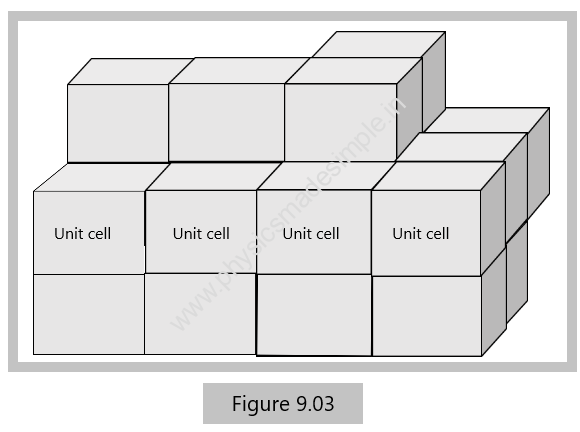
The entire structure of a crystal lattice has been observed to consist of identical blocks, which are known as unit cells. Therefore, the smallest building block or the geometrical figure using which the crystal is obtained by its repetition in three dimensions, is called a unit cell.
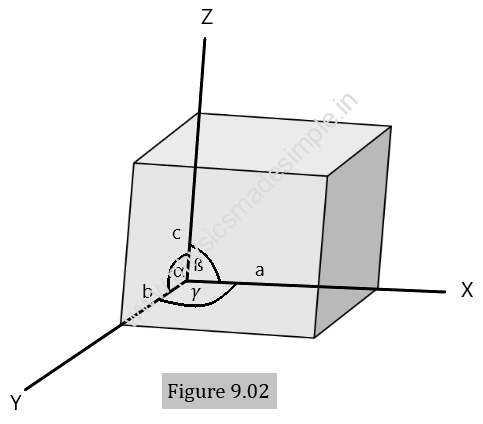
The unit cell, as shown in Figure 9.02, is a fundamental elementary pattern that forms the lattice structure of the crystal when repeated again and again in three dimensions. Some important terms related to the unit cell are listed below.
- Crystallographic axes: The lines drawn parallel to the lines of intersection of any three faces of the unit cell not lying in the same plane are called crystallographic axes. X, Y, and Z, as shown in Figure 9.02, are the crystallographic axes.
- Primitives: The primitives of a unit cell are its three sides, denoted by a, b, and c. These are also called lattice constants.
- Interfacial angles: The interfacial angles are defined as the angles between the three crystallographic axes of the crystal and are denoted by α, ß, and 𝛾.
With the help of primitives a, b, and c and interfacial angles α, ß, and 𝛾, the structure of a crystal is completely defined. As shown in Figure 9.03, by repeating a unit cell again and again, a three-dimensional crystal can easily be obtained.
Crystal systems:
In terms of the shape of the unit cells and corresponding to the different values of primitives, a, b, and c and interfacial angles α, ß, and 𝛾, all the crystals have been divided in to seven types of crystal systems. In the order of their growth, the seven types of crystal systems are discussed below.
1.Triclinic system:

For this type of crystal system, the primitives and the interfacial angles are related as a ≠ b ≠ c and α ≠ ß ≠ 𝛄 ≠ 90o. This is the crystal system with the maximum degree of asymmetry.
An elementary cell has a form of an oblique parallelopiped. Some standard triclinic systems include, copper sulfate, potassium dichromate, amazonite, kyanite, etc.
2. Monoclinic System:
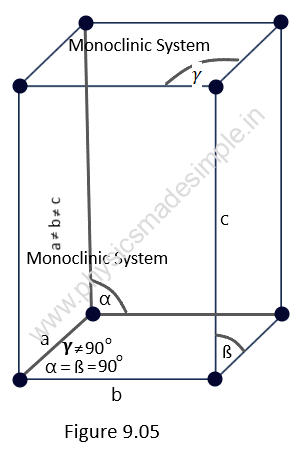
For this type of crystal system, the primitives and the interfacial angles are related as follows: a ≠ b ≠ c; and α = ß = 90o and 𝛄 ≠ 90o.
An elementary cell of a monoclinic system has the form of a right prism with a parallelogram at its base. It has three axes, of which two are at right angles to each other while the third is inclined, and all three primitives are different lengths.
For example: Na2 SO4, K ClO3, Fe SO4, etc.
3. Rhombic or Orthorhombic System:

For this type of crystal system, the primitives and the interfacial angles are related as follows: a ≠ b ≠ c; and α = ß = 𝛄 = 90o and thus, it consists of the three axes perpendicular to each other.
An elementary cell of an orthorhombic system has the shape of a rectangular parallelopiped.
For example: K NO3, gallium, mercury chloride, etc.
4. Tetragonal System:
For this type of crystal system, the primitives and the interfacial angles are related as follows: a = b ≠ c; and α = ß = 𝛄 = 90o and thus, it consists of the three axes perpendicular to each other.
An elementary cell has the form of a right prism with a square base. NiSO4, white tin, etc. are examples of this type of crystal system.
The two axes are of equal length and lie in the same plane, while the third axis, which is the main axis, may be short or long as compared to the other two.
5. Trigonal or Rhombohedral System:

For this type of crystal system, the primitives and the interfacial angles are related as follows: a = b = c; and α = ß = 𝛄 ≠ 90o.
An elementary cell of this type of system has the form of a deformed cube under the action of a force of compression or tension along the diagonal. Arsenic, Sb, Bi, calcite, etc. are examples of this type of crystal system.
6. Hexagonal System:

For this type of crystal system, the primitives and the interfacial angles are related as follows: a = b ≠ c; and α = ß = 90o and 𝛄 = 120o .
Three elementary cells come together to form a regular hexagonal prism. Zn, ZnO, Cd, Ni, etc. are examples of hexagonal systems.
7. Cubic System:
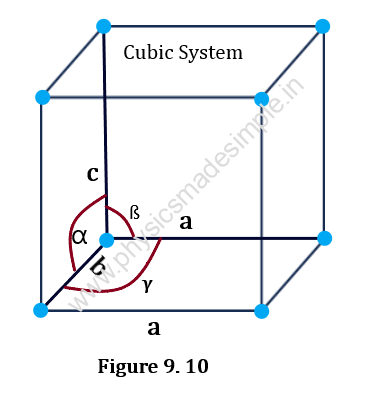
For this type of crystal system, the primitives and the interfacial angles are related as follows: a = b = c; and α = ß = 𝛄 = 90o.
An elementary cell has the form of a cube. NaCl, KI, Cu, etc. are examples of this type of crystal system.
In 1880, Bravais introduced the concept of space lattice, and according to him, there are 14 types of space lattices in the above seven crystal systems. It is therefore clear that there may be more than one Bravais lattice for the same crystal system.
cubic crystal system:
One of the seven fundamental crystal systems in mineralogy and crystallography is the cubic crystal system. The placement of atoms or ions in a symmetrical and geometrically simple three-dimensional lattice structure distinguishes it. The crystal lattice in the cubic system has three equal-length, mutually perpendicular axes that connect at right angles. Materials crystallizing in this system exhibit a number of unique features and behaviors thanks to this symmetry.
Simple cubic, body-centered cubic (bcc), and face-centered cubic (fcc) are the three primary varieties of cubic lattices found in the cubic system. These lattices vary in their constituent particle arrangements as well as their symmetrical properties.
- Simple cubic crystal:
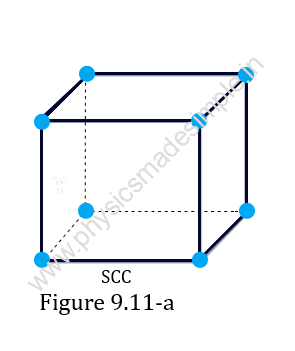
In this arrangement, each lattice point is positioned at the corners of a cube. It is the simplest and least dense packing arrangement, where each particle contacts six neighbors. Due to their low packing efficiency, materials with a simple cubic lattice are relatively rare. NaCl (sodium chloride) is one of the few examples of a simple cubic crystal structure.
The atom at a corner of the unit cell shares space with the eight different unit cells. Therefore, the effective number of atoms per unit cell of SCC is 8 x 1/8 = 1.
Figure 9.11-a shows a simple cubic cell (scc)
2. Body-centered cubic crystal:

In this type of arrangement, A lattice point in a body-centered cubic lattice occupies each corner of the cubic cell, and the cube’s center is also home to a lattice point. In comparison to a simple cubic lattice, this packing is more effective because each particle is in contact with eight neighbors. Examples of elements that crystallize in the bcc structure include iron, chromium, and tungsten.
The lattice point at the center of the unit cell of bcc completely belongs to that unit cell. Thus, the effective number of atoms per unit cell of BCC is 8 x 1/8 + 1 = 2 lattice points.
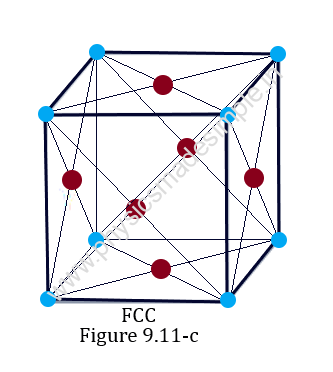
3. Face-centered cubic crystal:
The face-centered cubic lattice is the most densely packed among the cubic lattices. In this type of crystal, the unit cell is a cube with one lattice point (atom) at each of the eight corners in addition to one atom at the center of each face, as shown in Figure 9.11-c.
Therefore, the effective number of atoms per unit cell of FCC is 8 x 1/8 + 6 x 1/2 = 4 lattice points (or atoms).
As all three types of cubic crystals (scc, bcc, and fcc) are made of cubic unit cells, therefore `all primitives and the interfacial angles are the same, implying that, a = b = c and α = ß = 𝛄 = 90o. In a crystal system, the different Bravais lattices are differentiated from each other on the basis of their different values of atomic radius, coordination number, and atomic packing factor.
Materials that crystallize within the cubic crystal structure acquire particular properties. Isotropy, or the fact that physical qualities like elasticity, thermal expansion, and electrical conductivity are the same in all directions within the crystal lattice, is the most remarkable characteristic. Because of this, cubic crystals are homogeneous in their responses to external stimuli and relatively mechanically stable.
A distinctive symmetry is also seen in cubic crystals. With three 4-fold rotational axes running along each of the main crystallographic directions, they exhibit a remarkable level of rotational symmetry. The crystal is divided into symmetrical halves using mirror planes, and the cubic materials’ mechanical, electrical, and optical properties like diffraction, scattering, dispersion, and polarization are impacted by these symmetry elements.
Atomic radius:
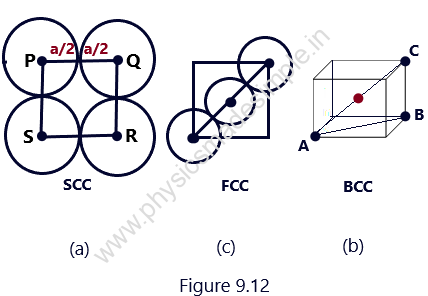
The atomic radius of the atoms packed in a unit cell is defined as half of the distance between the centers of the two neighboring atoms. It is also known as a lattice constant or lattice parameter.
Under the assumption that the atoms in a crystal are spheres of equal size touching each other, as shown in Figure 9.12. With the help of Figure 9.12, It can easily be calculated that the atomic radii of the atoms for SCC, BCC, and FCC are, respectively:
a/2, √3 a/2, and a/√2
Co-ordination number:
The coordination number of an atom in a crystal is defined as the number of nearest neighboring atoms that surround it. It can be proved easily that the co-ordination numbers of scc, bcc, and fcc are 6, 8, and 12, respectively, indicating that each atom in a simple cubic crystal is surrounded by 6 nearest atoms, each atom in a body-centered cubic crystal is surrounded by 8 nearest atoms, and each atom in a face-centered cubic crystal is surrounded by 12 nearest atoms.
Atomic packing factor:
The atomic packing factor is defined as the ratio of the volume occupied by all the atoms in a unit cell to the total volume of the cell.
Thus, APF = (volume of all the atoms in a unit cell/ volume of the cell)
For SCC:
f = n x 4/3 x (22/7) x (a/2)3 /a3 = (1 x 4 x22)/(3 x 7 x 8) = 88/168 = 0.523
For BCC:
f =n x 4/3 x (22/7) x (√3.a/2)3 /a3 = 0.68 similarly
For FCC:
f =n x 4/3 x (22/7) x (a/√2)3 /a3 = 0.74
single crystals (solids):
A single crystal is a crystalline substance in which the ordered arrangement of atoms or molecules throughout the entire solid extends.
Due to their anisotropy, single crystals exhibit directional differences in their mechanical, thermal, electrical, and optical properties like refraction of light, reflection of light, and interference of light. Depending on the system to which the crystal belongs, crystals have planar facets that are at an angle to one another. These crystals are easily cleaved along a few predetermined planes, or cleavage planes. On a path perpendicular to the cleavage planes, it is challenging to remove the crystal. It explains how the mechanical strength of a single crystal changes with respect to its orientation.
Additionally, a single crystal is typically relatively small in size. It ranges from a centimeter to a few centimeters. Monocrystals are very tiny crystals that have internal structures that are invisible to the unaided eye.
Poly Crystals:
The crystalline solids are comprised of polycrystals, which are collections of several monocrystals connected together by well-developed faces.
Polycrystals do not exhibit anisotropy or an orderly arrangement of atoms or molecules. It’s because huge crystals, which are collections of intergrown and randomly oriented fine crystals, are something we encounter in practice. Because nearby crystals have impeded their normal growth, the structure is asymmetrical and random. In polycrystals, anisotropy is only visible inside the boundaries of each tiny, individually taken crystal. A big single crystal can be produced by creating appropriate crystallization conditions in a solution or melt.
The polycrystal ceramic made from PbO, ZrO2, and TiO2 is used in gas lighters and telephone receivers. Ceramic oxides are usually bad conductors, but ceramics made from materials like Y2O3, BaO, and CuO2 exhibit superconductivity.
Liquid Crystals:
Liquid crystals are organic crystalline solids that retain their anisotropic properties while becoming fluid-like upon heating.
In certain temperature ranges, some organic crystalline solids develop a phase halfway between solid and liquid while retaining their anisotropy and long-range molecular orientational order.
Watches and microcalculators use liquid crystal displays (LCDs) that can alter the plane of polarization of light, such as alkyl cyanobiphenyl. The color of some substances in the liquid crystal phase changes with temperature, such as cholesterol esters. Liquid crystal thermometers are used to measure this characteristic.