Atomic nucleus-12 learn in fun

Atomic nucleus

The composition of an atomic nucleus has been the subject of controversy since a long time. The idea of an atomic nucleus came into existence after an experiment by Rutherford on the scattering of alpha particles from a thin gold foil of thickness equal to that of atomic size.  On the basis of the observations, he revealed that the nucleus is a central core of the atom wherein the entire mass of the atom is concentrated.

The composition of the atomic nucleus has been a subject of controversy for a long time. The study of radioactive disintegration shows that there is an emission of Alpha, Beta, and Gamma particles from the nucleus. Whereas the study of artificial radioactivity has revealed that there are many other particles like protons, neutrons, alpha particles, beta particles, and also the sub-particles like positrons, mesons, neutrinos etc. enter the constitution of the nucleus in one way or the other way. There were several hypotheses put forward about the structure of the atomic nucleus. Out of these hypotheses, the main two hypotheses are discussed here.

Proton-electron hypothesis:

In 1930, this hypothesis was put forward in order to explain the emission of alpha and beta particles from the atomic nucleus of radioactive elements. If A is the mass number and Z is the atomic number of an element then on the basis of this hypothesis, the nucleus of an atom of mass number A and atomic number Z, is made up of Z protons and (A – Z) electrons. Since the atom is observed to be electrically neutral, so, it must have Z additional electrons that revolve around the nucleus in circular orbits in order to maintain the charge neutrality of the atom. According to this theory,

• The emission of an alpha particle was equivalent to the emission of two electrons and four protons.
• The emission of beta particles was accounted for by the presence of electrons in the nucleus.
• The gamma rays were emitted from an excited nuclear state in the same way as the light was emitted from an excited state of the electron of an atom.

Failure of this hypothesis

(a) The existence of electrons inside the atomic nucleus could not be justified on the basis on the basis of wave mechanics.

(b) According to the de-Broglie hypothesis and Heisenberg’s uncertainty principle, for an electron to exist inside the atomic nucleus, it should have at least an energy ranging from 20 to 200 M eV.  But the energy of the electrons emitted during the beta-decay is almost 2 to 3 M eV. Therefore, the existence of electrons inside the nucleus could not be justified on the basis of wave mechanics.

(c)  Experimental values of magnetic moments of the nuclei were found to be much smaller than the magnetic movements of electrons they actually have. Therefore, the existence of the electrons inside the atomic nucleus is ruled out.

Proton-neutron hypothesis:

Heisenberg after the discovery of Newton, in 1932 by Chadwick, presented a nuclear model called the proton-neutron hypothesis. According to this hypothesis, a nucleus of mass number, A and atomic number Z, consists of Z protons and (A – Z) neutrons. The charge of the nucleus is positive due to the presence of protons in it (+Ze), while protons and neutrons together account for its total mass.

Therefore, protons and neutrons can be regarded as fundamental building blocks of matter. As an atom is electrically neutral, therefore, the number of extra-nuclear electrons in circular orbits around the atomic nucleus must be equal to Z, the number of protons inside the atomic nucleus. This hypothesis accounted for all the discrepancies of the proton-electron hypothesis as outlined earlier.

Nucleons:

A protons and neutrons are considered to be the two different states of the same particle are collectively called as nucleons.

Proton:

Proton is a fundamental particle and also a constituent of atomic nucleus and it carries a unit positive charge = + 1.6 x 10^-19 C and mass = 1.6729 x 10^-27 Kg = 1.007825 a.m.u. A proton has an intrinsic angular momentum =1/2 and it also possess a magnetic moment which is much smaller than the magnetic moment of an electron. However, its mass is about 1837 times the rest mass of the electron.

Neutron:

A neutron is also a constituent particle of atomic nucleus. It has no charge, but having mass slightly greater than that of proton. Its rest mass is equal to 1.6743 x 10^-27 Kg = 1.008665 a.m.u. It has an intrinsic angular momentum equal to that of a Proton. Although, it is a neutral particle having no charge, even then, it possess a small magnetic moment.

Neutrons and protons are identical particles in the sense that their masses are nearly the same and even the nuclear forces cannot distinguish them. So the neutrons and protons have the common name nucleons. The electromagnetic force can distinguish the two types of particles. as proton is positively charged and the neutron is neutral.

Characteristics of Atomic nucleus:

(1) Isotopes, Isobars, Isotones and Isomers:

A. Isotopes:

Nuclei with the same number of protons but different numbers of neutrons are called isotopes. Isotopes have similar chemical properties but may have different nuclear properties, such as stability and radioactive decay.

Bainbridge Mass Spectrograph as Isotopes Separator:

Ions are separated using mass spectrographs, which use the mass-to-charge ratio (m/z) to do so. They can be applied to a number of tasks, such as isotope separation, accurate mass measurements, and analysis of isotopic compositions.

The method of isotope separation entails separating and enriching particular isotopes of an element from a mixture. The manufacturing of isotopically enriched materials for use in industry and medicine, as well as nuclear research, isotope tagging for tracer investigations, and other scientific and industrial applications, all depend on this procedure.

Although I was unable to locate any specific information regarding the “Bainbridge mass spectrograph,” it is possible to convert many conventional mass spectrographs or mass spectrometers to separate isotopes by using various methods. Mass spectrometry is frequently used for isotope separation utilizing the following techniques

(1) Magnetic Sector Mass Spectrometry: In this method, ions are separated based on their mass-to-charge ratio using magnetic fields. Ions with different masses follow different curved paths in the magnetic field, allowing for their separation.

(2) Time-of-Flight (TOF) Mass Spectrometry: In TOF mass spectrometry, ions are accelerated through an electric field and separated based on their velocities, which are related to their masses. Lighter ions reach the detector faster than heavier ions.

(3) Quadrupole Mass Spectrometry: Quadrupole mass spectrometers use a combination of static and oscillating electric fields to selectively transmit ions with specific mass-to-charge ratios. By tuning the applied voltages, specific isotopes can be isolated.

(4) Ion Cyclotron Resonance (ICR) Mass Spectrometry: ICR mass spectrometry utilizes a magnetic field to trap ions in a cyclotron motion. The frequency of this motion is related to the mass-to-charge ratio of the ions, allowing for their separation and identification.

For example:

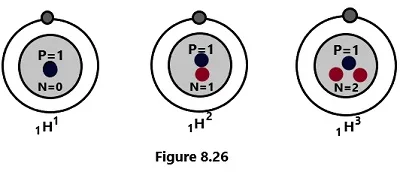
(1) ₁H¹ , ₁H² and ₁H³ are the isotopes of hydrogen.

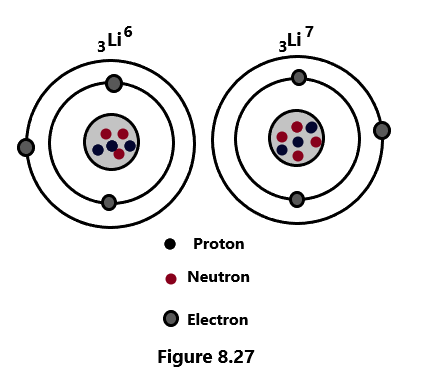
(2) ₃Li⁶ and ₃Li⁷ are the isotopes of lithium

(3) ₈O¹⁶, ₈O¹⁷ and ₈O¹⁸ ; ₉₂U²³⁵ and ₉₂U²³⁸ are the isotropic forms of oxygen and uranium respectively.

B. Isobars:

Isobars are the nuclei that have the same mass number but different atomic numbers. In other words, they are atoms of different elements that have the same total number of nucleons (protons + neutrons) in their nuclei. Isobars always have different atomic structure due to the difference in atomic numbers and they are always different chemical elements having same atomic mass.

For example:

(1) ₂₆Fe⁵⁸ and ₂₈Ni⁵⁸ are the isobaric nuclei

(2) ₁H³ and ₂He³ are the isobaric nuclei

(3) ₁₇Cl³⁷ and ₁₆S³⁷ are the isobaric nuclei

Properties of isobaric nuclei:

Isobaric nuclei find applications in various fields. For instance, in mass spectrometry, isobaric interference can occur when different elements have the same mass-to-charge ratio, leading to challenges in accurate elemental analysis. Isobaric tagging is also used in proteomics to differentiate peptides with the same mass but different compositions, aiding in the identification and quantification of proteins.

Isobaric nuclei provide insights into nuclear structure, decay processes, and the behavior of different elements. Understanding their properties is crucial for applications in fields like nuclear physics, chemistry, and analytical sciences.

(C) Isotones:

Isotones are nuclei that have the same number of neutrons but different numbers of protons. In other words, isotones are atoms of different elements that have the same neutron number. For example: ₁₇Cl³⁷ and ₁₆S³⁶ are the isobaric nuclei.

Properties of isotonic nuclei:

(1) Neutron Number (N): Isotones have the same neutron number (N), which represents the total number of neutrons in the nucleus. For example, oxygen-16 (₈O¹⁶) and fluorine-17 (₉F¹⁷) are isotones because they both have a neutron number of 8.

(2) Different Proton Numbers (Z): Isotones have different proton numbers (Z), indicating that they belong to different elements. The proton number determines the element’s identity and influences its chemical behavior and properties.

(3) Nuclear Structure: Isotones provide insights into nuclear structure and the interplay between protons and neutrons. By studying isotones, scientists can observe how changes in proton numbers affect the properties and behavior of nuclei while keeping the neutron number constant. This helps in understanding the nature of nuclear forces and the organization of nucleons within the nucleus.

(4) Applications in Nuclear Physics: Isotones play a significant role in nuclear physics research. They are used to study various nuclear phenomena, such as nuclear reactions, fission, and fusion. By examining isotones, scientists can investigate the behavior of specific combinations of protons and neutrons, leading to a deeper understanding of nuclear processes.

(5) Applications in Astrophysics: Isotones are also relevant in astrophysics and nuclear astrophysics. They help scientists understand stellar nucleosynthesis, the process through which elements are formed in stars. By studying isotones, researchers can analyze the nuclear reactions occurring in stars and explain the abundance of certain isotopes observed in the universe.

(6) Nuclear Energy and Reactor Design: Isotones have implications in nuclear energy and reactor design. Different isotones have different neutron absorption and fission cross-sections, which affect their behavior in nuclear reactors. Understanding isotones is crucial for optimizing reactor designs, fuel selection, and managing nuclear waste.

(7) Isotone Mapping: Isotone mapping involves studying the properties and behavior of isotones across the periodic table. This mapping provides insights into the systematic trends of nuclear properties, such as nuclear size, binding energy, and stability. Isotone mapping helps identify regions of enhanced stability and regions where nuclear reactions are more likely to occur.

Isotones are valuable tools for studying nuclear structure, nuclear reactions, astrophysical processes, and practical applications in nuclear physics and energy. By examining isotones, scientists can deepen their understanding of the atomic nucleus and its interactions.

(2) Atomic mass: ;

The atomic mass of an atomic nucleus, also known as the mass number (A), is the total number of nucleons (protons and neutrons) present in the nucleus of an atom. It is expressed in atomic mass units (a.m.u) or unified atomic mass units (u).

The atomic mass an atomic nucleus is determined by summing the individual masses of the protons and neutrons in the atomic nucleus. The mass of a proton is approximately 1.007825 a.m.u, while the mass of a neutron is also close to 1.008665 a.m.u. Since electrons have negligible mass compared to protons and neutrons, they are not included in the atomic mass calculation.

To calculate the atomic mass, you simply add the number of protons (Z) and neutrons (N) together:

Atomic Mass (A) = Number of Protons (Z) + Number of Neutrons (N)

For example, the atomic mass of carbon-12 is 12 AMU because it contains 6 protons and 6 neutrons. Similarly, the atomic mass of oxygen-16 is 16 AMU, with 8 protons and 8 neutrons.

Unit of atomic mass: The atomic mass of an element is measured in atomic mass unit (1 a.m.u.) One atomic mass unit is defined as 1/12th of the mass of one carbon atom of mass number 12 (C-12), Thus.

1 a.m.u = 1/12 x mass of one ₆C¹² atom = 1/12 x (12/6.023 x 10²³) gm = 1.66 x 10^-24 gm => 1 a.m.u = 1.66 x 10^-27 Kg

Electron Volt:

Electron volt is the unit of energy and is defined as the energy gained by a moving electron when it is accelerated through a potential difference of one volt. Hence,

1 eV = 1.602 x 10^-19 C x 1 V= 1.602 x 10^-19 J

1 M eV = 1.602 x 10^-13 J

Relation Between a.m.u. ang M eV

Using Einstein’s mass energy relation,

E = m c²

= 1 a.m.u. x (3 x 10⁸ m s^-1)² J

= 1.49 x 10^-10 J

= [1.49 x 10^-10 /1.602 x 10^-19] eV

= [1.49 x 10^-10 /1.602 x 10^-13] M eV = 931.5 M eV

1 a.m.u = 931.5 M eV

It’s important to note that the atomic mass listed on the periodic table for an element is usually an average value called the atomic mass or atomic weight. This is because different isotopes of an element have varying numbers of neutrons, resulting in slightly different atomic masses. The weighted average of the masses of all naturally occurring isotopes of an element, taking into account their relative abundances is represented by the atomic mass on the periodic table. Atomic masses can be measured accurately by using an instrument called a mass spectrometer.

Size of an atomic Nucleus:

The physical dimensions of an atomic nucleus, represent its size which is the central part of atoms having maximum density. The size of a nucleus is simply measured in the form of its radius or the diameter. The nature of its internal structure and the inherent challenges in experimental measurements has made it a complex task to determine the exact size of a nucleus.

One of the simple and primary methods used to determine the size of an atomic nucleus is through scattering experiments as Rutherford did. A beam of particles, such as electrons or other atomic nuclei, is directed toward a target nucleus in most of these types of experiments, The way in which the particles scatter off the target provides information about its size. By analyzing the scattering patterns and applying theoretical models, the size and shape of the atomic nucleus can be determined.

The experimental observations reveals that the volume of a nucleus is directly proportional to the mass number A, thus,

4/3 . π R³ ∝ A ⇒ R ∝ A^1/3

R = R₀A^1/3

Where R₀ = 1.2 fm is constant and depends upon the probe particles. Since, the mass number A is different for different elements, therefore, the atomic nuclei of different elements have different sizes.

The role of nuclear size in nuclear reactions:

Nuclear reactions are highly dependent on the size of an atomic nucleus. The size of an atomic nucleus has a significant impact on the many features of nuclear reactions, such as the likelihood that a nuclear reaction will occur and the nuclear reaction cross-section (a measure of the interaction intensity) for a specific reaction. Due to their bigger size and increased surface area, larger nuclei generally have a higher likelihood of participating in nuclear processes. The precise specifics, however, depend on the nature of the reaction and the characteristics of the interacting particles.

For instance, in nuclear fusion reactions, where two lighter nuclei combine to form a heavier atomic nucleus, the size of the nuclei plays a significant role. The closer the nuclei can come together, the higher the probability of fusion. Larger nuclei typically require higher temperatures and pressures to overcome electrostatic repulsion and bring the nuclei close enough for fusion to occur.

In nuclear fission, the splitting of a heavy atomic nucleus into two or more lighter nuclei, the size of the atomic nucleus is also relevant. The larger the nucleus, the more likely it is to undergo fission, as the repulsive forces within the nucleus become stronger with increasing size. Additionally, the size of the fission fragments can impact subsequent reactions, such as the release of energy and the production of new neutrons, which can sustain a chain reaction.

The size of an atomic nucleus is experimentally determined by the technique including scattering experiments as performed by Rutherford. The nuclear scale plays a key role in nuclear reactions by influencing the likelihood and cross-section of processes like nuclear fusion and nuclear fission. The kinetics and outcomes of such events, as well as the conditions that must exist for reactions to occur, are all influenced by the sizes of the implicated nuclei.

nuclear density

By nuclear density, we mean the density of the nuclear matter of an atom. It is defined as the mass per unit volume inside the nucleus. Since the atomic nucleus carries most of the atom’s mass and the size of the atomic nucleus is very small in comparison to that of the entire atom, the nuclear density is very high. As the volume of the nucleus is directly proportional to the mass number so the density of nuclear matter is independent of the mass number or size of the nucleus.

Let us suppose that A is the mass number, and R is the radius of the nucleus, if the average mass of nucleon is m, then the mass of nucleus equal to mA.