Bohr’s atom model
This atom model accounts for the stability of the atom and the line spectrum exhibited by the hydrogen atom. Consequent upon the failure of Rutherford’s atomic model to explain the stability of the atom and the line spectrum of hydrogen atom, Neil Bohr, in 1913, presented a new atomic model, called as Bohr’s atom model. The followings are the postulates of this model.
Postulates of Bohr’s atom model:
Neil Bohr made some assumptions in 1913, regarding the atomic constitution, called as the postulates of Bohr’s atom model which are given as below.
(1) Quantized Energy Levels: Bohr proposed that electrons in hydrogen atoms can only occupy certain specific energy levels, known as stationary states or orbits. Each of these orbits is associated with a fixed energy value. Electrons can transition between these energy levels by either absorbing or emitting energy in the form of photons.
Every atom consists of a central core called nucleus in which entire positive charge (+Ze) and mass of the atom are concentrated. The same number of electrons revolve around the nucleus in circular orbits as the number of protons in the nucleus. The necessary centripetal force required for the circular motion of the electron around the nucleus is provided by the electrostatic force of attraction between the electrons and nucleus. (Bohr’s atom model)
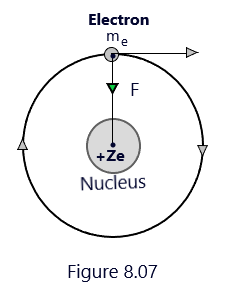
Thus, centripetal force = Electrostatic force of attraction on the electron by the nucleus

(2) Angular Momentum Quantization: Bohr postulated that the angular momentum of an electron in a stationary state is quantized. The angular momentum (L) is given by the product of the electron’s mass (m), orbital velocity (v), and the radius of the orbit (r).
The electrons are allowed to revolve round the nucleus only in those circular orbits in which the angular momentum of the electrons is an integral multiple of h/2π, where h is the Plank’s constant. Thus, the angular momentum of orbiting electron is quantized. and is given by,
mvr = n (h/2π) – – – (ii).
where n = 1, 2, 3, 4, —– is an integer and is called as Principal quantum number. Therefore, the electrons can revolve only in those orbits in which the angular momentum of the electros are,
(h/2π), 2(h/2π), 3(h/2π), – – – -.
These orbits are called as allowed stationary state. (Bohr’s atom model)
(3) An electron revolves around the nucleus with a definite fixed energy in a circular path of fixed radius known as stationary states without gaining or losing the energy. The stationary states of the electron is known as energy level. (Bohr’s atom model)
(4) Emission and Absorption of Photons: The energy is radiated, when an electron jumps from higher to lower energy orbit and energy, is absorbed when it jumps from lower to higher energy orbits or energy levels. (Bohr’s atom model)
If Ei and Ef are the energies associated with the orbits of the principal quantum numbers Ni and Nf, respectively, then, the energy radiated out in the form of a photon is given by,
hv = Ef – Ei
Thus, the frequency (f) of the emitted photon is related to its energy through Planck’s equation and hence, each transition between energy levels corresponds to a specific frequency (or wavelength) of the emitted photon. (Bohr’s atom model)
Application of bohr’s theory on hydrogen atom:
By applying these postulates, Bohr successfully explained the line spectrum of hydrogen. Each observed line in the spectrum corresponds to a specific transition of an electron between different energy levels. The wavelengths and frequencies of these lines can be calculated using the quantized energy levels of the hydrogen atom, as described by Bohr’s theory. However, it’s important to note that Bohr’s model is limited to hydrogen-like species and doesn’t fully explain the behavior of more complex atoms. The theory was later superseded by the more comprehensive quantum mechanical model of the atom.
In the hydrogen atom, there is only one electron of charge -e, and revolves round the nucleus of charge +e, in a circular orbit of radius r. As per the first postulate of Bohr’s atom model, The necessary centripetal force = mv2/r is provided by the electrostatic force of attraction, so that

According to the postulate of quantization condition in Bohr’s atom model, the angular momentum of the electron is
mvr = n h/2π or v = n h/2π m r – – – (iv)
Putting the value of v from eqn. (iv) in (iii), we get

Since, n = 1, 2, 3, 4, – – – – – -, then, from eqn. (v), it is evident that the radii of the non-radiating stationary states are proportional to n2, implying that the radii of the non-radiating stationary states increase in the ratio 1: 4: 9: 16 – – – – – –
The velocity of the electron in an orbit is determined using eqns. (iv) and (v), so

It is clear from the above equation that the speed of an electron in an nth orbit is inversely related to the Principal quantum number n. Therefore, an electron goes slower and slower as around the nucleus in the orbits corresponding to the higher and higher value of n. (Bohr’s atom model)
Bohr radius:
The radius of first orbit, corresponding to n =1 in a hydrogen atom is called as Bohr radius (r0). It is obtained by putting n=1 in eqn. (v). Thus, we have
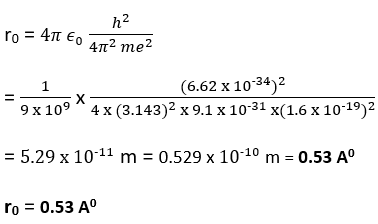
Speed of Electron:
The speed of the electron in an orbit in the hydrogen atom is obtained using eqn. (vi) as follows
v = 2πk e2/nh = (2πk e2/ch) . c/n = α c/n – – – –(vii)
The term α = (2πk e2/ch) is constant and dimensionless and is called as fine structure constant. Its value is calculated as
α = (2 x 3.143 x 9 x 109 x (1.6 x 10-19)2/3 x 108 x 6.62 x 10-34)=1/137
Therefore, v = (1/137). c/n ⇒ v = c/137, for first orbit, n =1 – –viii
Therefore, the speed of the electron in the innermost orbit or the first orbit is one (1/137)th part of the speed of light in vacuum, where as the speed of the electron in outer orbit varies inversely with n. (Bohr’s atom model)
Energy of Electron:
The total energy of an electron in the nth orbit of hydrogen atom is the sum of its kinetic energy and potential energy in that orbit. Thus,
EN = EK + EP – – – – – (ix)

This gives the total energy of an electron in the nth orbit of hydrogen atom. The negative value of energy indicates that there exists an electrostatic force of attraction which keeps the electron bound to the nucleus and to take it away from the nucleus, some external work has to be done to do so. (Bohr’s atom model)
Energy quantization:
The total energy of an electron in the nth orbit is given as

Putting different quantum values of principal quantum number n=1, 2, 3, 4, . . . . . . . .
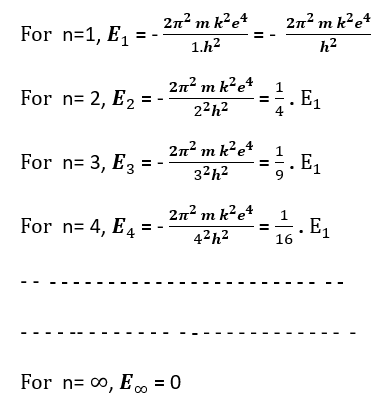
As is seen here that the energy of an electron is not continuous but is discrete. The energy values of the electron is definite in different quantum states corresponding to n=1, 2, 3, .. . . . . This is called as energy quantization. (Bohr’s atom model)
The energy of the electron is minimum in the first orbit and the electron has zero energy when it is at infinite distance from the nucleus. The energy states corresponding to n = 1, is called as ground state, whereas the states corresponding to n n= 2, 3, 4, . . . . ., are called excited states. When the electron is to be raised from ground state (n = 1) to excited states (n = 2, 3, 4, . . . . . , then energy is to be supplied to the electron. On the other hand, when electron jumps from some higher energy state to the ground state or from an outer level to the inner level, the jump of electron is accompanied by the emission of energy. (Bohr’s atom model)
.
Spectral series of hydrogen atom:
The spectral series of the hydrogen atom refers to the specific wavelengths of light emitted or absorbed by a hydrogen atom when electrons under go transition between different energy levels. These transitions give rise to characteristic spectral lines in the electromagnetic spectrum. The study of these spectral lines was crucial in the development of quantum mechanics and provided important insights into the structure of atoms. According to the Bohr’s theory, the energy of the electron in the nth orbit of hydrogen atom is given by equation (x). (Bohr’s atom model)
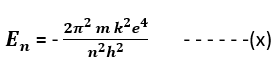
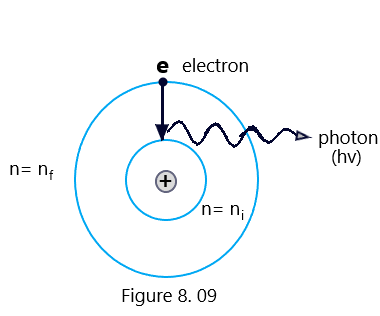
It has been credited to Bohr’s frequency condition that when an electron in an atom makes transition from some higher energy level nf to the lower energy level ni then the difference in the energy appears in the form of radiation of particular wavelength. The frequency of the emitted radiation is given by (Bohr’s atom model)

The equation (xi) gives the wave number (reciprocal of wavelength) of the photons emitted as a result of transition of electron from higher energy states to ground energy state. (Bohr’s atom model)
The major spectral series of the hydrogen atom include:
(1) Lyman series: This series corresponds to electron transitions from some higher energy states to the nf=1 energy level (ground state). The emitted or absorbed wavelengths fall in the ultraviolet region of the spectrum. The first line in the Lyman series (n=2 to n=1) is known as Lyman-alpha and has a wavelength of 121.6 nanometers.
(2) Balmer series: In the Balmer series, electron transitions from other higher energy states to the nf=2 energy level. The emitted or absorbed wavelengths are in the visible spectrum. The first line in the Balmer series (ni=3 to nf=2) is known as H-alpha and has a wavelength of 656.3 nanometers, falling in the red part of the spectrum.
(3) Paschen series: This series involves transitions from other higher energy states to the nf=3 energy level. The emitted or absorbed wavelengths are in the infrared region. The first line in the Paschen series (ni = 4 to nf = 3) has a wavelength of 1875.1 nanometers.
(4)Brackett series: Brackett series corresponds to transitions from other higher energy states to the nf=4 energy level. The emitted or absorbed wavelengths are in the infrared region. The first line in the Brackett series (ni =5 to nf =4) has a wavelength of 4051.6 nanometers.
(5) Pfund series: This series involves transitions from other higher energy states to the nf=5 energy level. The emitted or absorbed wavelengths are also in the infrared region. The first line in the Pfund series (ni=6 to nf=5) has a wavelength of 7458.9 nanometers.
These are just some of the series that make up the hydrogen atom’s spectrum. Each series consists of multiple spectral lines corresponding to different electron transitions between energy levels. (Bohr’s atom model)
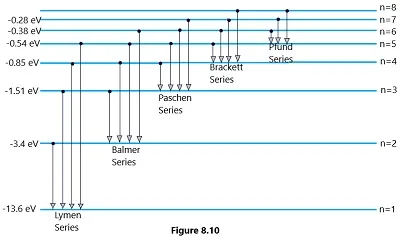
It’s worth noting that the spectral lines are a direct consequence of quantized energy levels in the hydrogen atom, as described by Bohr’s atom model and later developed by quantum mechanics. The energy levels of the hydrogen atom are given by the formula: E = -13.6 eV/n2, where ‘n’ is the principal quantum number. As electrons transition between these quantized energy levels, they emit or absorb photons with specific energies and wavelengths, leading to the observed spectral lines. (Bohr’s atom model)
Energy level Diagram of hydrogen atom
The energy level diagram of the hydrogen atom is a graphical representation of the allowed energy states that an electron can occupy within the atom. It is one of the fundamental concepts in quantum mechanics and provides insight into the electron’s behavior and the emission or absorption of photons. (Bohr’s atom model)
In a hydrogen atom, which consists of a single proton in the nucleus and one electron orbiting around it, the electron’s energy is quantized. This means that the electron can only exist in specific energy levels or states, and transitions between these levels are accompanied by the emission or absorption of photons with specific energies. In the energy level diagram, the vertical axis represents the energy of the electron, and the horizontal axis represents the different energy levels or shells labelled as n=1, n=2, n=3, and so on, where n is the principal quantum number. (Bohr’s atom model)
The energy levels in the hydrogen atom are quantized, meaning that only certain specific energies are allowed for the electron. These energy levels are determined by the principal quantum number n. (Bohr’s atom model)

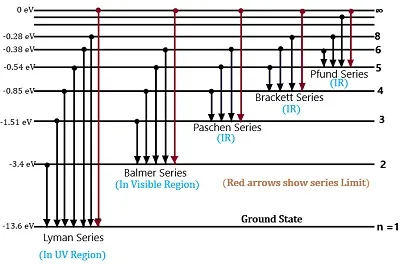
where E is the energy of the electron and -13.6 eV is the ionization energy of hydrogen. Thus, the energy level diagram of the hydrogen atom as a graphical representation of the allowed energy states that an electron can occupy within the atom appears as follows. (Bohr’s atom model)
The energy level diagram is typically represented with the energy increasing upwards on the y-axis, and the quantum numbers on the x-axis. The principal quantum number, denoted by ‘n,’ represents the main energy level or shell that the electron occupies. It has integer values starting from 1 (ground state) and goes upwards. The higher the value of ‘n,’ the higher the energy level and the farther the electron is from the nucleus. (Bohr’s atom model)
Limitations of Bohr’s Atom Model:
Bohr’s atomic model, proposed by Niels Bohr in 1913, was a significant advancement in understanding the structure of atoms. However, it also had some limitations. Here are the main limitations of Bohr’s atom model:
Failure to explain complex spectra: Bohr’s model successfully explained the spectral lines of hydrogen, but it struggled to explain the spectra of more complex atoms with multiple electrons. The model could not account for the fine details and complexities observed in the spectra of other elements.
Incomplete understanding of electron behavior: According to Bohr’s model, electrons move in circular orbits at fixed energy levels or shells. However, later scientific developments, such as quantum mechanics, revealed that electrons do not follow strictly circular paths but rather exist in electron clouds around the nucleus, described by probability distributions.
Neglect of electron-electron interactions: The model neglected the electrostatic repulsion between electrons. In reality, electrons repel each other due to their negative charges, which affects their behavior and energy levels. This limitation became more apparent when studying atoms with multiple electrons.
Lack of a theoretical basis: Bohr’s model was developed based on empirical observations rather than a theoretical framework. It lacked a solid foundation in fundamental principles and mathematical derivations, which limited its ability to provide a comprehensive understanding of atomic structure.
Limited applicability to other atoms: The model was primarily applicable to hydrogen-like atoms, which have only one electron. It struggled to explain the behavior of elements with more complex electron configurations, such as transition metals or heavier elements.
Inconsistency with the Heisenberg uncertainty principle: Bohr’s model suggested that electrons have definite positions and velocities, which contradicted the Heisenberg uncertainty principle. According to quantum mechanics, it is impossible to simultaneously determine both the precise position and momentum of a particle.
Lack of explanation for chemical bonding: Bohr’s model did not provide an explanation for the nature of chemical bonding and the formation of molecules. It focused mainly on the behavior of individual atoms, rather than their interactions and the forces involved in chemical reactions.
Despite these limitations, Bohr’s model was an essential step in the development of quantum mechanics and helped pave the way for more sophisticated models, such as the quantum mechanical model, which provides a more accurate and comprehensive understanding of atomic structure.
Numerical Problems:
Problem 01:
Calculate the speed of the electron in the n =2 orbit of Helium atom.
Solution: Given here, n = 2, and z = 2 for helium atom ( 2He4 )
Using the relation for the speed of electron in hydrogen like atom, vn = k (2π) Ze2/nh
= 9 x 109 x 2 x 3.143 2 x (1.6 x 10-19)2/(2 x 6.62 x 10-34)=2.19 x 106 m s-1
=> v2 = 2.19 x 106 m s-1
Problem 02:
Show that the speed of an electron in the innermost orbit of H- atom is (1/137) times the speed of light in vacuum.
Solution: The speed of the electron in the innermost orbit of H- atom is:
v = k (2π) Ze2/h
v = k (2π) Ze2 c/ch
v = 9 x 109 x 2 x 3.143 2 x (1.6 x 10-19)2 c/[2 x (6.62 x 10-34)] x 3 x 108 = (1/137) c
MCQs:
Q. 01
The total energy of electron in nth stationary orbit of hydrogen atom is
(a) 13.6/n2 eV
(b) 13.6/n2 joule
(c) – 13.6/n2 eV
(d) – 13.6/n2 joule
Q. 02
In which region of electromagnetic spectrum does the Lyman series of hydrogen atom lie?
(a) X-Rays
(b) UV- Region
(c) Infrared Region
(d) Visible- Region

2 Comments