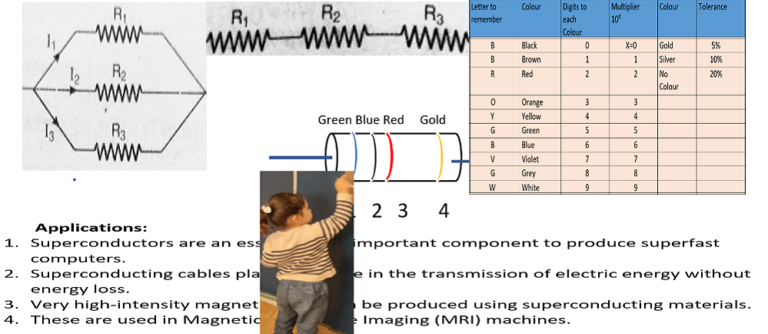
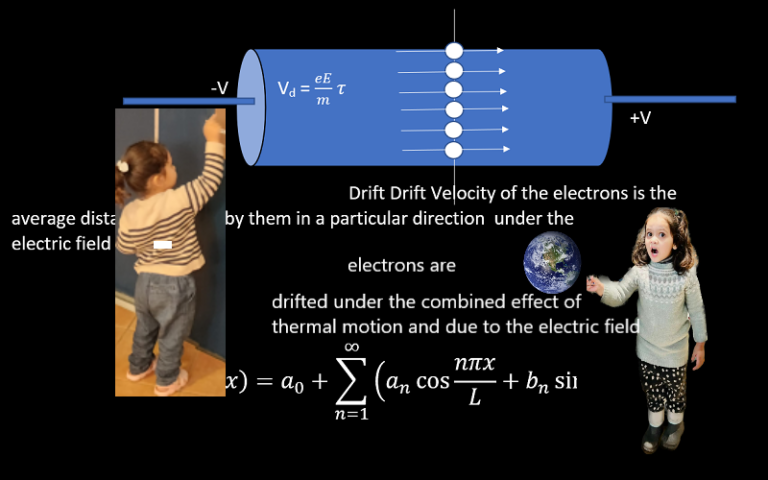
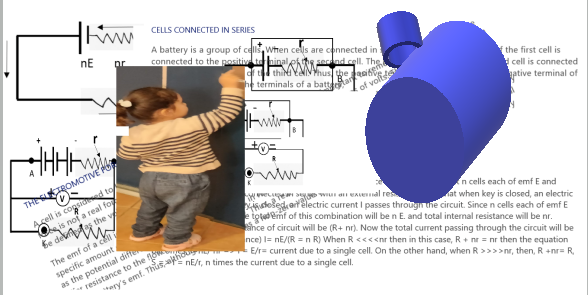
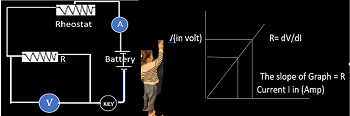
Cylindrical Capacitor-12
A cylindrical capacitor-12 consists of two co-axial cylindrical shells, such that one shell is earthed and the other is used to store charge on it.
Cylindrical Capacitor-12-Construction
A cylindrical capacitor consists of two co-axial cylindrical shells, such that one shell is earthed and the other is used to store charge on it. The two cylindrical shells have a very small spacing between them, which is fixed with some dielectric medium or left with air or consists of a vacuum depending upon the use, it is to put for.
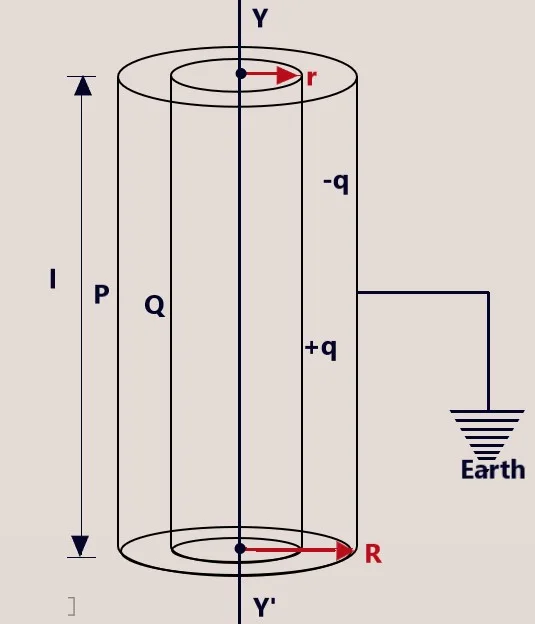
Expression for capacitance of a cylindrical capacitor-Cylindrical Capacitor-12
From the figure given above, we see that the cylindrical capacitor consists of two cylindrical shells P & Q with r & R be their respective radii and L be the length of the cylindrical shells. When a charge +q is given to the inner cylindrical cell Q, a Charge equal to -q is induced on the inner surface of the cylindrical shell P and charge +q on its outer surface. As the shell P is earthed, the induced charge, +q on the outer surface flows to Earth. If. V is potential difference between the cylindrical cells, P & Q, then the capacitance of the capacitor is given by.
C = q / V – – – 01
Now, the electric field In the space between the two cylindrical shells is also not uniform. Therefore, if electric field at any point P at a distance, R. From the axis of the cylindrical cells is east, then potential difference between the two cells is given by
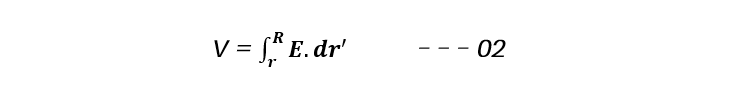
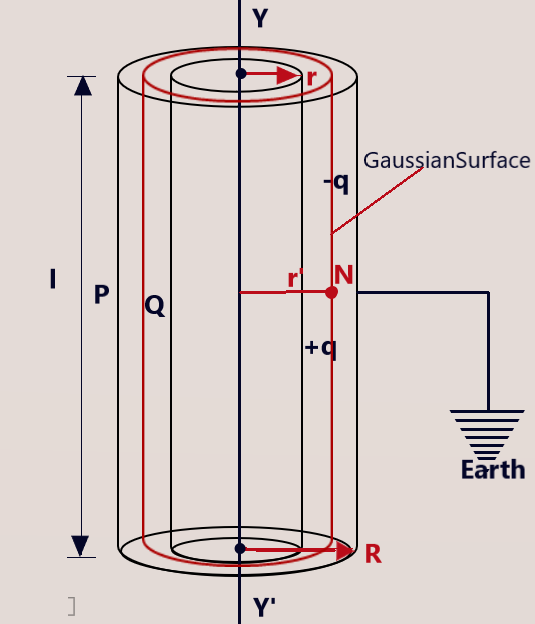
In order to find the value of electric field intensity at any point N in the space between the two cylindrical shells, we consider an imaginary gaussian cylindrical surface such the the experimental point N lies at the surface of the gaussian surface as shown in the figure highlighted in red color. Let us suppose that E is the electric field intensity at point P on the surface of Gaussian cylinder of radius r’. Now applying Gauss’s Law, the total electric flux through the gaussian surface will be

Since, the electric field intensity is uniform in magnitude at every point on the gaussian surface, therefore, we can write the total electric flux through the gaussian surface as the product of the magnitude of electric field intensity and the surface area of the gaussian surface, thus


The capacitance of the cylindrical capacitor-12 per unit length if the capacitor is expressed as
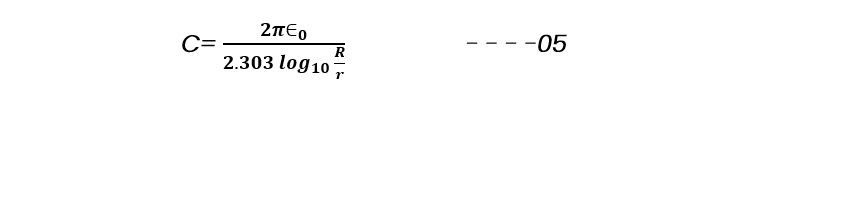
The above equation 05 gives the capacitance of a cylindrical capacitor per unit its length having r and R as the radii of inner and outer cylinders with the air or vacuum filled in space between these co-axial cylinders. When the space between these co-axial cylinders is filled with a dielectric medium of dielectric constant K, then the Eqn.05 can be rewritten as

From the above Eqn. 06, it is clear that the capacitance of a cylindrical capacitor increases by K times ( K is the dielectric constant of the dielectric medium) when a dielectric medium is inserted between the two co-axial cylinders constituting a cylindrical capacitor-12.
Cylindrical Capacitor-12-Key points and concepts
- on introduction of dielectric slab, the potential difference between the plates of a capacitor decreases by a factor equal to K(dielectric constant of the dielectric medium)
- Since battery remains connected to the capacitor, potential difference across the cylinders remains equal to the battery voltage.
- The electric field between the two co-axial cylinders in a cylindrical capacitor is not uniform.
- The electric capacitance of the cylindrical capacitor strongly depends upon the radii of the two co-axial cylinders.