Electromagnetic waves-12 Learn in Fun Enjoy

Electromagnetic waves-12

What are Electromagnetic waves?

Two fields mutually perpendicular time varying electric and magnetic fields constitute electromagnetic waves which propagate in space in the direction perpendicular to the directions of both the fields.

Definition of Electromagnetic Waves

Electromagnetic waves consist of sinusoidally time-varying electric and magnetic fields acting at right angles to each other, as well as at right angles to the direction of propagation of the electromagnetic energy.

In the beginning, Maxwell tabled the idea of electromagnetic waves, while Hertz and other scientists studied the concepts and the existence of these waves experimentally and produced the results. In 1865, Maxwell predicted the existence of electromagnetic waves on the basis of his observations. According to him, an accelerated charge particle produces a sinusoidal time-varying magnetic field, which in turn produces a sinusoidal time-varying electric field. The two fields so produced are mutually perpendicular and are the sources of each other. The mutually perpendicular time-varying electric and magnetic fields constitute electromagnetic waves, which propagate in space in a direction perpendicular to the direction of both fields.

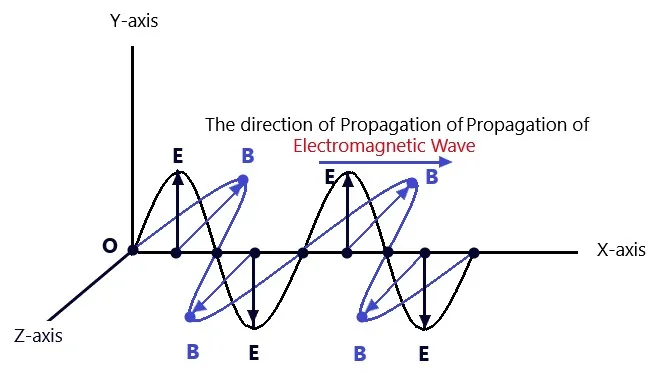
As shown in Fig. The electric field vector E is along Y-Axis, while the magnetic field vector B is along Z-Axis. The propagation of the electromagnetic field is in the direction of the vector (E x B). Since the electric and magnetic fields are perpendicular to each other and to the direction of wave propagation, electromagnetic waves are transverse in nature. The speed of electromagnetic waves in free space is given by

Characteristic’s of electromagnetic wave

1. Transverse Nature of Electromagnetic wave

An electromagnetic wave consists of time-varying electric and magnetic fields, which are mutually perpendicular to each other, as well as to the direction of the propagation. Electromagnetic wave is transverse in nature. In order to establish the transverse nature of electromagnetic wave, we shall prove that both electric and magnetic fields are perpendicular to each other and perpendicular to the direction of wave propagation

Consider a plane electromagnetic wave propagating along the positive direction of the X- axis and a rectangular parallelopiped ABCDEFGH placed with its edges parallel to the three-coordinate axis as shown in the figure. The electric and magnetic fields change sinusoidally with X and t only and are independent of y and z directions.                                                                                                      

According to Gauss’s law, as the parallelopiped does not include any charge. Therefore, the total net electric flux across it must be zero.

From Eqn. 04 it is implied that either E_x = E_x^‘ = 0 or E_x = E_x^‘, The second possibility that E_x = E_x^‘ is ruled out as this shows that the electric field is static and cannot propagate as wave. The first possibility that E_x = E_x^‘ = 0 implies that this component of electric field along the direction of propagation is zero. It means , the electric field is perpendicular to the direction of propagation of wave. On similar pattern, it can be proved that the magnetic field is also perpendicular to the direction of the propagation of the wave.

Therefore, The electromagnetic waves are perpendicular to the direction of both the fields, electric as well as magnetic field. This shows that these waves are transverse in nature.

2. Speed of Electromagnetic Wave

(a) To Prove c=(E₀/B₀)

Let us suppose that a closed rectangular path PQRS in X-Y plane is placed in the path of an EM Wave propagating along X – axis as shown in the figure below

Now, we can apply here the Faraday’s law of electromagnetic induction which states that the line integral of an electric field taken over a closed path (PQRS) is equal to the rate of change of magnetic flux through the area enclosed by the closed path.

In order to find the magnetic flux through the area enclosed by the rectangle PQRS, we suppose an elementary strip of width dx and at a distance x from the origin as shown in the figure above, then the magnetic flux through the strip will be

(b) To find the speed of EM waves in terms of absolute permeability and absolute permittivity of free space

In order to find the expression for speed of EM waves in terms of absolute permeability and absolute permittivity of free space, let us consider a closed rectangular path ACDN in X-Z plane in the path of electromagnetic waves propagating along X axis as shown in the fig. According to Maxwell’s ampere’s circuit in law, the line integral of magnetic field along the closed path ACDN is equal to absolute permeability  times the sum of conduction and displacement currents, threading the area enclosed by the path ACDN. Because, there is no conduction current in space,

The electric flux through the area enclosed by the rectangle ACDN is determined by taking an elementary strip of width dx at a distance x from the origin, as shown in the figure, if E(x) is the value of the electric field at the elementary strip, then electric flux through the strip will be.

3. Average Energy Density of Electromagnetic Waves

As the time varying Electric and Magnetic fields are the essential constituents, so it is customarily fact the the total energy of an electromagnetic wave is equally shared amongst the constituent fields. Thus, the average electric energy density of EM wave in vacuum is given by

4. Poynting Vector and intensity of Electromagnetic waves

Poynting Vector: The propagation of the electromagnetic waves in space is associated with the transport of energy. This energy transported by electromagnetic waves per second per unit area is represented by a vector quantity called  poynting vector and it is denoted by

The magnitude of the poynting vector gives the energy transported by the EM waves per second per unit area and the direction of the this vector gives the direction in which the energy is transported and is perpendicular to electric as well as magnetic field.

Intensity of electromagnetic waves: Intensity of electromagnetic waves is defined as the energy passing through a unit area of a surface in each second when the surface is held perpendicular to the direction of propagation of the electromagnetic wave. It is denoted by I and in terms of poynting vector, it is given by

Properties of electromagnetic waves

• Electromagnetic waves propagate in the form of varying electric and magnetic fields such that the two fields are perpendicular to each other and also to the direction of propagation of the wave. In other words, electromagnetic waves are transverse in nature.
• These waves are produced by accelerated charges.
• The EM waves don’t require any material medium necessarily for their propagation. These waves can propagate in air in vacuum or in a any other material medium.
• In free space the EM waves travel with the velocity equal to that of light in free space and is given by 3 x 10⁸ meter per second.
• The electromagnetic wave obeys the principle of superposition.
• The electric vector is responsible for the optical effects like refraction, diffraction reflection and polarization etc. due to an electromagnetic wave for this reason, the electric vector is called light vector.
• The time variations in the amplitudes of electric and magnetic fields in the electromagnetic wave always in same phase, it implies that these changes take place at the same time and at the same point in the space. Thus, the ratio of the amplitudes of electric and magnetic fields is always constant, and it is equal to velocity of the electromagnetic waves. Mathematically, we can write, (E₀ / B₀)= c
• The energy in electromagnetic wave is shared equally amongst the electric field as well as magnetic field vectors.
• The momentum transportation takes place during the propagation of the electromagnetic wave and the momentum transported by these waves is p= U/c, U is the energy of the EM wave and c is its velocity of propagation of these waves. As a result, the pressure is exerted by them on the surfaces when these waves strike the surfaces.
• The energy transported by the EM waves per second per unit area is represented by a vector quantity called poynting vector.

Key points of the electromagnetic waves

• The electromagnetic waves of all types are transverse in nature, it means that an electromagnetic wave is propagated in the direction perpendicular to the directions of the electric and magnetic fields
• The direction of Propagation of an electromagnetic wave is given by the cross product of electric field and magnetic field vectors.
• The frequency of electromagnetic wave is its inherent characteristic that when an electromagnetic wave travels from one medium to another, it’s wavelength changes out, but its frequency always remains unchanged.
• All the types of electromagnetic waves travel with the same speed in free space as. That of the light 3 x 10⁸ m/s
• When the electromagnetic wave strikes a surface. It exerts pressure on the surface on which it strikes
• Maxwell’s equations are the mathematical formulations of Gauss’s law in electrostatics and Gauss’s law in magnetism. Faraday’s law of electromagnetic induction and Ampere’s circuital law.
• The conduction current and displacement current are entirely different from each other. However the displacement current produces magnetic field in the same manner as the conduction current does.