Huygens Principle
Introduction To Wave Optics
The ray optics assuming that the light travels in a straight line except at the interface separating two media, provides the useful information and explains the phenomena like, reflection, refraction and rectilinear propagation of light to the level of satisfaction. However, there are other microscopic phenomena like, interference, diffraction, polarization which, the concept of ray optics could not be explain. The concept of wave optics was introduced to explain these phenomena. This new branch of optics was called as wave optics. (Huygens Principle)
Various Theories about the nature of light have been proposed from time to time but some main theories regarding the nature of light are discussed here. (Huygens Principle)
Newton’s Corpuscular Theory of light
This theory of light was presented by Sir Isaac Newton in 1627 A.D. According to this theory any luminous body emits the light in the form of tiny particles called Corpuscles. These energy particles are emitted by the source in all possible directions. Newton’s Corpuscular Theory of light could explain the phenomena of reflection, refraction and rectilinear propagation of light but could not explain the phenomena of interference, diffraction and polarization of light.
Wave theory of light
After the failure of Corpuscular theory in 1678, a Dutch scientist Christian Huygens, proposed that the light energy traveled from one place to another in the form of wave motion. He suggested that light travels in the form of longitudinal wave, just as sound propagates through air. He proposed that there exists a medium called ether, which fills every empty space in the universe. (Huygens Principle)
He had to assume the presence of this hypothetical medium as wave motion requires a medium for its propagation. The color of the light depends upon the wavelength of light. Later on, the existence of such a medium was discarded due to its contradictory properties. Fresnel and young showed that light propagates in a transverse waves. With the help of this theory, reflection, refraction, interference and diffraction were successfully explained. (Huygens Principle)
Huygens Principle It gives a method to know as to how the light spreads out in the medium. Huygens Principle is a geometrical construction, which is used know position of a wave front at a later time from its given position at any instant of time. The following are the assumptions which Huygens Principle is based upon. (Huygens Principle)
* Every point on the primary wavefront acts as a fresh source of secondary wavelets and sends out the disturbances in all possible directions exactly in same way as the original source of light does.
*The line joining the secondary wavelets in forward direction at any instant of time, represent the position of the secondary wavefront at that instant of time.
These two assumptions given above are called Huygens’ principle or Huygens’ geometrical construction of wavefront.
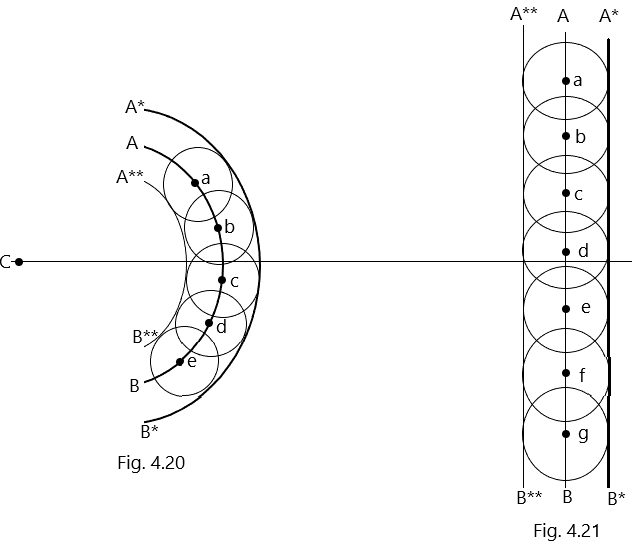
Let us suppose that a point source is placed at point C and sends out energy vibrations in all the directions. Consider that AB is a section of primary spherical wavefront at any time t. In order to find the recent position of the wavefront at a time (t + dt), we consider different points a, b, c, d, – – – – – on the primary wavefront AB as shown in [Fig. 4.20].
As per first assumption, these points will act as the fresh sources of secondary wavelets. In time dt, the light travels a distance equal to (c. dt). Assuming these points a, b, c, d, – – – – – as the centers, we draw the spheres each of radius (c. dt). These spheres represent the secondary wavelets originating from these points on the primary wavefront. Now the lines joining these secondary wavelets A*B* and A**B** in forward and backward directions are the envelops which represent the secondary wavefronts. (Huygens Principle)
Huygens assumed that the portion of the secondary wavelets lying on the backward secondary wavefront A**B** are nonexistent as the energy does not flow in backward direction. Voigt and Kirchhoff, proved mathematically a few years later that the contribution of the wavelets to the intensity in any direction is proportional to 1/2 [1 + cos(theta)], where theta is the angle which the wavelet makes with the normal to the wavelets. (Huygens Principle)
It is clear that the angle (theta) is equal to 180o for the portion of the wavelet lying on the backward secondary wavefront A**B**. This leads to the fact that for the angle (theta) is equal to 180o , the the contribution of the factor 1/2 [1 + cos(theta)] towards the intensity is zero. Therefore, this leads to the conclusion that the forward secondary wavefront A*B* is the position of the new wavefront at a time (t + dt) (Huygens Principle)
In similar way, the new position of of a cylindrical or a plane wavefront can be found. In Fig. 4.21 AB represents the primary plane wavefront and A*B* represents the new position of the wavefront at a time (t + dt). (Huygens Principle)
Wavefront and its Types
According to the principles of wave theory of light, a source of light when switched on, sends out the disturbances in all the directions which in a homogenous medium, reach all the equidistant points from the source of light in phase. Therefore, all such particles at any instant of time are observed to be vibrating in same phase with each other.
The wavefront is defined as the locus of all the particles of the medium which vibrate in same phase at any instant of time.

Spherical Wavefront: When the source of light is a point source, then the wavefront associated with the wave is said to be a spherical wavefront because the locus of all the point which are equidistant from a point source lie on the surface of the sphere as shown in [Fig. 4.22(a)] and the particles lying on the surface of this sphere vibrate in same phase. (Huygens Principle)
Cylindrical Wavefront: When the source of light is a line source, then the wavefront associated with the wave is said to be a cylindrical wavefront because the locus of all such points which are equidistant from a linear source lie on the surface of the cylinder as shown in [Fig. 4.22(b)] and the particles lying on the surface of this cylinder vibrate in same phase. (Huygens Principle)
Plane Wavefront: A small portion of the spherical or cylindrical wavefront originating from a point source or a linear source like a slit at infinitely larger distances appears as a plane and hence called as a plane wave front as shown in [Fig. 4.22(c)]
It is observed that the disturbance travels outwards along the straight lines emerging from the source irrespective of the shape of the wavefront(may be spherical, cylindrical, and plane wave front). Thus, the energy of the wave travels in a direction perpendicular to the wavefront. Therefore, an arrow drawn normal to the wavefront and pointing in the direction of propagation of disturbance represents the ray of light. (Huygens Principle)
Reflection of light on the basis of wave theory
laws of reflection on the basis of wave Theory:
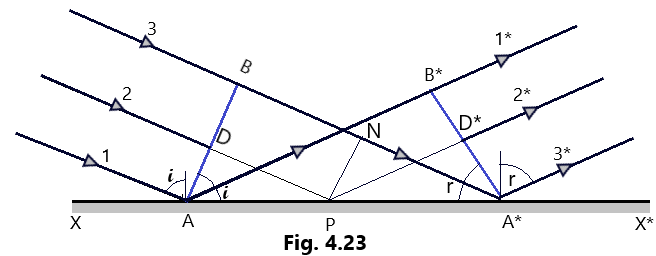
Let us suppose that a plane wavefront AB is allowed to incident on a plane mirror XX*. so that the angle BAA* is the angle of incidence and 1, 2, 3 are the corresponding incident rays perpendicular to to the wavefront AB. As per the assumption of Huygens’ Principle, each point on this wavefront AB act as the independent source of secondary wavelets. If the secondary wavelets originating from point B reaches the point A* in time t second, then BA*= c .t – – – – (01).
In similar way, the secondary wavelets from the point A will travel the same distance in time t so that AB*= c .t – – –(02) As it is clear from Fig. 4.23, A*B* is the secondary wavefront after a time t and 1*, 2*, 3* are the corresponding reflected rays normal to the secondary wavefront A*B*. It is also true and evident that the secondary wavelets starting from the incident wavefront AB and from any point say D, after reflection at point P, must reach the point D* on the wavefront A*B* in the same time. (Huygens Principle)
Therefore, A*B* is truly considered as the reflected wavefront as shown in Fig. 4.23. and from this, it is also evident that in the two triangles BAA* and B*AA*, BA* = AB* Angles AB*A*= ABA*= 90o each and AA* is common to both the triangles. Hence, these two triangles are similar and congruent implying that the angle i = angle r. This is the condition of reflection of light. (Huygens Principle)
It is also evident here that the incident wavefront AB, the reflected wavefront A*B*, and the reflecting surface XX* all lie in same plane and are also perpendicular to the plane of the paper. This implies that the incident ray, the reflected ray and the normal to the mirror all lie in the same plane which is the plane of the paper. This gives the second law of reflection. Thus, both of the two laws of reflection are explained perfectly. (Huygens Principle)
Refraction of light on the basis of wave theory
laws of refraction on the basis of wave Theory:
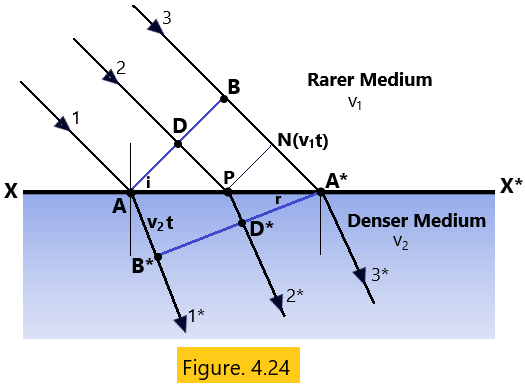
Let us consider that XX* is an interface separating two media of different densities. A plane wavefront AB is incident on this interface XX* separating a denser medium of refractive index (mu) from air which is the rarer medium and the rays marked with 1, 2, and 3 are the corresponding incident rays. Let us further suppose that v1 and v2 are the velocities of the light wave in the rarer and the denser medium respectively such that v2 < v1 so that the refractive Index = v1 /v2 – – -(03)
As per the assumption of Huygens’ Principle, each point on this wavefront AB act as the independent source of secondary wavelets. If the secondary wavelets originating from point B reaches the point A* in time t second, then BA*= v1 .t – (04) The distance covered by the secondary wavelets from point A in the denser medium will be v2 t. As shown in Figure 4.24, note that A*B* is the secondary wavefront after a time t second and the ray marked with 1*, 2*, and 3* are the corresponding refracted rays. (Huygens Principle)
It can also be proved that the secondary wavelets from any point on the primary wavefront AB (say from point D) after suffering refraction at point P, must reach the point D* on the secondary wavefront A*B* exactly in the same time as taken by the secondary wavelets from point B to reach the point A*. Hence AB* is the new and refracted wavefront. The angle of refraction is the angle which the refracted plane wavefront A*B* makes with the surface XX* and is given by r so that angle AA*B*= r, the angle of refraction. From the triangle AA*B, (Huygens Principle)

The above result is an evident proof of Snell’s Law. This also implies that the incident ray, the refracted ray and the normal to the interface all lie in the same plane which is the plane of the paper. This gives the second law of refraction. Thus, both of the two laws of refraction are explained perfectly. (Huygens Principle).
Effect on The wavelength, Frequency and the speed during Refraction
The time taken by a beam of light to travel from a source at res in one medium to the observer at rest in some other medium when there is no relative motion between the two media keeping the geometry of the source, medium and observer unchanged with time. Let us suppose that a source emits a wavefront after every time interval of T second each wavefront takes a time T second to reach the observer from the source. Then the number of wavefronts received by the observer per second is called frequency which is given by n= (1/T). This implies that the frequency (n) remains constant as light travels from one medium to another medium=>(n1 = n2).
Since the speeds of the light v1 and v2 are different in different media of different densities and nature, therefore, the wavelength associated with the light wave in different media must also be different. Thus, The absolute refractive index can be written as

The Eqn. (06) given above shows that the wavelength of a light wave in a medium is directly proportional to the speed of the wave in that medium and inversely proportional to the refractive index of the medium. The absolute refractive index of the medium can be written as

It is clear from above discussion that the speed of light in an optically rarer medium is greater than that in optically denser medium. (Huygens Principle)
behaviour of a prism, A Lens, and a spherical mirror towards the plane wavefront
When a plane wavefront is incident on a prism, a lens and a mirror the refracted and reflected wave fronts is not purely the plane but may be observed as the tilted plane wavefront and the spherical wavefront.
Behaviour of a Prism: Let us suppose that a plane-wavefront is incident on a thin prism of angle A. As the speed of light is smaller in glass than in air so the lower part K of the wavefront is slowed down the most than than the upper part M which travels through min. thickness of the prism. This is the reason that the tilting of a plane wavefront after refraction takes place through a glass prism as shown in Figure 4.25(A)
Behavior of Convex Lens: Consider that a plane wavefront MNK is incident on a convex lens. As per Huygens’ principle, each point on wavefront MNK, acts as the source of secondary wavelets. The refraction of plane wavefront through a convex lens is shown as in Figure 4.25(B) The emerging wavefront is spherical and converges to the focal point of the convex lens.

Behaviour of a concave Mirror: Let us suppose that a plane wavefront MNK is allowed to incident on the concave mirror as shown in Figure 4.25(C) As per Huygens’ principle, each point on wavefront MNK, acts as the source of secondary wavelets. In this case, the central part N of the incident wavefront travels more distance before getting reflected from the mirror as compared to the marginal parts M and K. Thus, the central part N* of the reflected wavefront is closer to the mirror than the marginal portions M* and K*. Thus, the reflected wavefront is spherical and converges to the focus point F
key points to remember
*The phase difference between any two points on a wavefront is always zero. (Huygens Principle)
*The Cylindrical wavefront is produced by a line source or a slit source while the Spherical wavefront is produced by a point source. The plane wavefront is produced when the light source is situated at infinitely large distance irrespective of the type of source (point source or line source). (Huygens Principle)
A ray of light is always normal to the WAVEFRONT (Huygens Principle)
*Huygens’ Principle is simply a geometrical construction to ascertain the position of the wavefront at some later time. (Huygens Principle)
*The effective part of the secondary wavelets is the front portion of the secondary wavefront. The contribution of the secondary wavelets on the back of the secondary wavefront is zero due to the reason that the energy flow in backward direction is not possible.
*A phase change of pi (180o) is introduced in a beam of light when it undergoes reflection at a point backed by a denser medium and no phase change takes place when a wave undergoes refraction.
