Maxwell’s Displacement Current-12
In order to over come the inconsistency in ampere’s circuital law, the concepts of displace current came into existence.

According to Ampere’s circuital law, the line integral of the magnetic field taken over a closed path or circuit is equal to the absolute permeability of free space times the total current enclosed in that closed circuit. This law is capable enough to obtain the results related to various electric circuits with great ease. But this law seems to be incomplete when applied to an electric circuit containing a capacitor as one of the basic circuit elements. J. C. Maxwell, introduced the concept of displacement current in order to overcome this inconsistency.
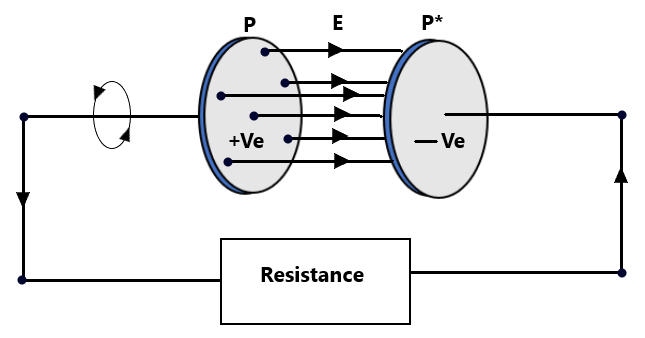
Suppose that a charged parallel plate capacitor is made to discharge through resistance as shown in fig.01, The current I leave the left face of the plate P of the capacitor flows through the conducting wire, and then enters the right face of the plate P* of the capacitor. The current flowing through the conducting wire is called the conduction current. As current cannot flow, through the space between the two plates of the capacitor, no current exists between these two plates. However, the electric field E exists in the space between the plates. Also, magnetic field B is set up around the conducting wire due to the flow of current through it.
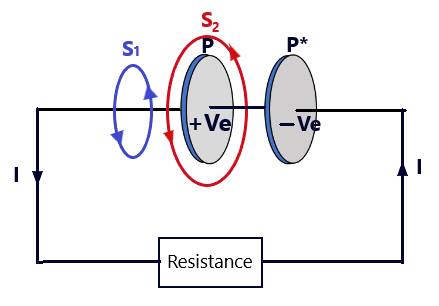
In order to discuss the inconsistency of the ampere circuit in law, let us consider two surfaces, S1 and S2, very close to each other and bound by the same loop. The two surfaces, S1 and S2 are held in such a way that the conduction current I, threads the surface S1 only, and the surface S2 passes through the space between the two plates of the capacitor, without touching the plates. We, now apply Ampere’s circuital law to both cases turn by turn.
When Ampere’s Circuital Law is applied to surface S1 (-Maxwell’s Displacement Current-12) As the conduction current, I is threading this surface, applying Ampere’s law to it, will lead to the line integral of the magnetic field produced due to the conduction current I can take the form as

When Ampere’s Circuital Law is applied to surface S2 (-Maxwell’s Displacement Current-12) This surface is very close to surface S1 and also bounded by the same loop but no current threads it. Thus, Ampere’s circuital law will take the form as follows.

The comparison of the equations 02 and 03 reveals that the two equations are not equal as their R. H. S are different. This leads to establish the inconsistency of Ampere’s circuital law, when the electric circuit includes a capacitor. Maxwell modified the Ampere’s circuital law through the introduction of the concept of displacement current to overcome the inconsistency.
Modified Form of Ampere’s circuital law /(Maxwell’s Displacement Current-12)
Maxwell interpreted the inconsistency of Ampere’s circuital law in terms of the wrong assumption that no current flows across the space between the two plates of the capacitor. Therefore, there is a discontinuity in the flow of current in such an electric circuit. In fact, it is not so, if a small compass needle is placed in the gap between the two plates of the capacitor, it shows deflection indicating the existence of a magnetic field.
So as to explain the existence of a magnetic field between the plates, Maxwell assumed the flow of current across the gap between the plates of the capacitor also. He named it displacement current – Maxwell’s Displacement Current-12, and attributed its origin to the time-varying electric field, between the plates of the capacitor. Thus. According to Maxwell, the varying electric field between the plates of the capacitor gives rise to the magnetic field.
Maxwell’s concept of displacement current -Maxwell’s Displacement Current-12makes a continuous flow of current in such an electric circuit. Thus, through the conducting wire, there is the flow of conduction current IC but no displacement current and through the gap across the place of the capacitor, there is a flow of displacement current ID but no conduction current.
The conduction current and the displacement currents, in a circuit, are always equal. Maxwell, on the basis of his findings, concluded that the current I in Ampere’s circuital law should be threaded as the sum of the conduction current IC and the displacement current ID. In the light of this conclusive theory presented by Maxwell, Ampere’s circuital law was modified as

This Eqn. 04 is called Ampere-Maxwell’s circuital law/modified form of Ampere’s circuital law and here, ID is called the displacement current that comes into existence due to time varying electric field between the plates of the capacitor and is written as

equivalence between conduction current and Maxwell’s Displacement Current-12
Consider that q is the instantaneous value of the charge on the positive plate of the capacitor at an instant of time t and the electric field across the space between the plate of the capacitor at the same instant of time is E, and the area of each plate is A, then we can write,

Key points of consistency of Ampere’s circuital law and – Maxwell’s Displacement Current-12
The followings are the key points and the conclusions that can be drawn from the above discussion.
- The conduction current IC and the displacement current ID are individually discontinuous but the two currents together exhibit the property of continuity through any closed electric circuits.
- The displacement current is precisely equal to the conduction current when the two are present in different parts of the circuit.
- The displacement current arises due to rate of change of electric flux or electric field. Between the two plates of the capacitor.
- Just as the conduction current is, the displacement current is also the source of magnetic fields.-Maxwell’s Displacement Current-12
The conduction current produces magnetic field due to change in motion, whereas the Maxwell’s Displacement current-12 produces magnetic field due to the time rate of change of electric field, thus, in the space between the plates of the capacitor, both the electric and the magnetic fields exist. The time varying electric field between the plates of the capacitor is directed perpendicular to the plane of the plates and the time varying magnetic field produced by the electric field is along the parameter of a circle in a plane parallel to the plate of the capacitor as shown in figure 03.
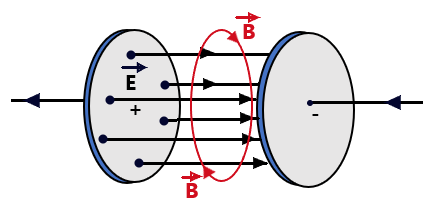
Thus, the time varying electric field (E) and magnetic field (B) are perpendicular to each other. The two fields combine to constitute an electromagnetic wave, which propagate in space in a direction perpendicular to the direction of both the fields with a speed given by

As it had been done earlier that the ratio of the amplitudes of the electric and magnetic fields is a constant and is equal to the speed of electromagnetic waves. Thus, the origin of the electromagnetic waves is very much connected with the concept of Maxwell’s Displace current-12.
maxwell’s Field equations
There are four basic laws in physics in terms of electric and magnetic fields namely called – (1) Gauss’s Law in electrostatics (2) Gauss’s Law in magnetism (3) Faraday’s Laws of electromagnetic induction (4) Ampere’s circuital law, were formulated and presented in mathematics were presented by Maxwell, which are called as Maxwell’s equations. These Maxwell’s equations predict that the time and space dependent electric and magnetic fields propagate as transverse waves, called electromagnetic waves, with a velocity equal to that of light. (c = 3 x 108 m s-1)

Summary
- In an electric circuit having a charged capacitor, the electric current flowing through the connecting wires is called conduction current while that flowing through the gap between the plates of a capacitor is called displacement current.
- The conduction and displacement currents are entirely different from each other. However, the displacement current produces magnetic field in the same manner as the conduction current does.
- The Displacement Current has its origin as the time varying electric field between the two plates of a charged capacitor.
- Maxwell’s equations are mathematical formulation of Gauss’s law in electrostatics, Gauss’s law in magnetism, Ferriday’s law of electromagnetic induction and Ampere’s circuital law.
Test your Knowledge
[HDquiz quiz = “72”]