N.C.E.R.T. Textual Questions-UNIT 6/Optics
It consists of the solutions to the N.C.E.R.T TEXTUAL Questions-UNIT 6/Optics for 12th class-Physics
Q. 6.01. N.C.E.R.T. Textual Questions-UNIT 6/Optics
A small candle 2.5 cm in size is placed 27 cm in front of a concave mirror of radius of curvature of 36 cm. At what distance from the mirror should a screen be placed in order to obtain a sharp image? Describe the nature and size of the image. If the candle is moved closer to the mirror, how would the screen have to be moved? (From N.C.E.R.T. Textual Questions-UNIT 6/Optics)
ANSWER:
Given that, u = – 27 cm, the size of the object, O = 2.5 cm, and f = R/2 = -36/2 = -18 cm Now using the relation, 1/u + 1/v = 1/f => 1/v = 1/f – 1/u = 1/ (-18) – 1/ (-27) = – 1/54 => v = – 54 cm Thus, the image will be real in nature and the screen should be placed at a distance of 54 cm from the mirror on the same side as that of the object. . Also, we can use the equation, I/O = – (v/u) or I/2.5 = -( -54/ -27) = -2 => I = 2 x – 2.5 = – 5 cm (Inverted Image)
The conclusion can be drawn that image formed will be real and inverted and it will move away from the mirror and likewise the screen has to be moved away in order to bring the image on the screen with the remarks that when the candle is at a distance less than 18 cm, the image formed will be virtual. In that situation, it is not possible to bring the image to the screen
Q. 6.02. N.C.E.R.T. Textual Questions-UNIT 6/Optics
A 4.5 cm needle is placed 12 cm away from a convex mirror of focal length 15 cm. Give the location of this image and the magnification. Describe what happens as the needle is moved farther from the mirror. (From N.C.E.R.T. Textual Questions-UNIT 6/Optics)
ANSWER:
Given that, u = – 12 cm, the size of the object, O = 4.5 cm, and f = + 15 cm Now using the relation, 1/u + 1/v = 1/f => 1/v = 1/f -1/u = 1/15 – 1/(-12) =9/60, or v = 60/9 = 6.67 cm ( Virtual Image) Also, using the relation, I/O = – (v/u) => I/4.5 = -[6.67/(-12)] = 5/9 => I = (5/9) x 4.5 = 2.5 cm (Erect) When the needle is moved farther from the mirror, the image also moves away from the mirror, but it will not go beyond the focus of the mirror.
Q. 6.03. N.C.E.R.T. Textual Questions-UNIT 6/Optics
A tank is filled with water to a height of 12.5 cm. The apparent depth of a needle lying at the bottom of the tank is measured by a microscope to be 9.4 cm. What is the refractive index of water? If water is replaced by a liquid of a reflective index, of 1.63 up to the same height, by what distance would the microscope have to be moved to focus on the needle again?(From N.C.E.R.T. Textual Questions-UNIT 6/Optics)
ANSWER:
When the tank is filled with water, we are given, Real depth = 12.5 cm, Apparent depth: = 9.4 cm, so we can write for Ref. Index, n = Real depth / apparent depth = 12.5/9.4 = 1.33 => n = 1.33: Also, when the tank is filled with liquid, we are given: Real depth = 12.5 cm, Ref. Index, n = 1.63; then Apparent depth = Real depth/ Ref Index = 12.5/ 1.63 = 7.67 cm. Therefore, the distance through which, the microscope is to be moved to focus the needle again = 9.4 – 7.67 =1.73 cm
Q. 6.04. N.C.E.R.T. Textual Questions-UNIT 6/Optics
Figs.- 6.04 (a) and (b) show the refraction of a ray in incident at 60o with the normal to a glass-air interface respectively. Predict the angle of refraction in glass, when the angle of incidence in water is 45o with the normal to a water-glass interface[ Fig.6.01(c)]
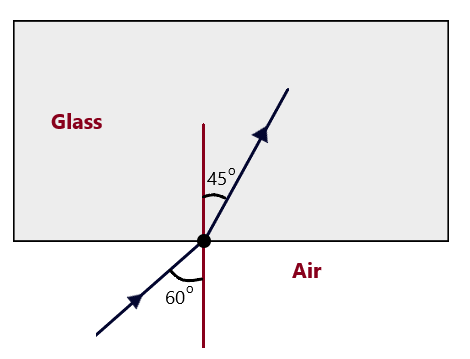


ANSWER:
In Fig. 6.01 (a): Given, i =60o and r = 35o, therefore, ang = Sin i/Sin r = Sin 60o / Sin 35o = 0.8660/ 0.5738 =1.51 and In Fig. 6.01 (b), Given, i = 60o and r = 41o, therefore, anw = Sin i/ Sin r = Sin 60o / Sin 41o = 0.8660/0.6560 = 1.32, Also now In Fig. 6.01 (c): Given, i =45o and r =? therefore, wng = ang / anw = 1.51/1.32 = 1.144, Also, wng = Sin i/ Sin r = 0.7071/Sin r, equating the two values, 0.7071/Sin r = 1.144 => Sin r = 0.7071/1.144 = 38.18 => r = 38.18O
Q. 6.05. N.C.E.R.T. Textual Questions-UNIT 6/Optics
A small bulb is placed at the bottom of the tank containing water to a depth of 80 cm. What is the area of the surface of water through which light from the bulb can emerge out? The refractive index of water is 1.33. Consider the bulb to be a point source.

SOLUTION:
Point L shows the position of the bulb at the bottom of a tank containing water of refractive index 1.33, up to the height h = 80 cm. The light will emerge out through the largest area, therefore, through a circle of maximum radius OA = OB = r, if on refraction at the water-air interface, it comes out parallel to the surface [Fig. 6.02]. (-N.C.E.R.T. Textual Questions-UNIT 6/Optics)
It will happen so, if the angle of incidence for the rays of light, incident at the points on the circumference of the circle of radius r, is equal to the critical angle for liquid-air interface, if. If C is the critical angle, then, n = 1/ Sin c => Sin C = 1/n = 1/1.33 = 0.7519 => C = 48.76o, from the right-angled triangle AOL, we have, tan C = OA/OL = r/h => r = h tan C = 80 x tan 48.76o – 80 x 1.1407. Thus, the required surface area through which the light from the bulb can come out = 3.143 x (91.256)2 = 26162.1 cm2 (-N.C.E.R.T. Textual Questions-UNIT 6/Optics
Q. 6.15. N.C.E.R.T. Textual Questions-UNIT 6/Optics
Use the mirror equation to deduce that. (a) an object placed between f and 2f of a concave mirror produces a real image beyond 2f. (b) a convex mirror always produces a virtual image independent of the location of the object. (c) the virtual image produced by a convex mirror is diminished in size and is located between the focus and the pole. (d) an object placed between the pole and the focus of a concave mirror produces a virtual and enlarged image. (N.C.E.R.T. Textual Questions-UNIT 6/Optics)
ANSWER:
(a) When an object is placed between f and 2f of a concave mirror implies that 2f > u > f (in magnitudes only), then we can write from the mirror formula, v = u f / (u – f). Since 2f > u > f, therefore, it is evident that v will be negative and v > 2f. Thus, it is inferred that a real image is formed beyond 2f for an object placed between f and 2f for concave mirror. (-N.C.E.R.T. Textual Questions-UNIT 6/Optics
(b) Let us suppose that an object is placed before a convex mirror. As we can write from the mirror formula, v = u f / (u – f). As per the new sign conventions, the distance of the object for the convex mirror is negative and the focal length is positive. Thus, the value of v will be positive and less than the value of u and f irrespective of the value of u. Therefore, a convex mirror always produces a virtual image independent of the location of the object. (-N.C.E.R.T. Textual Questions-UNIT 6/Optics)
(c) As we know that the distance of the object from the convex mirror is negative and the focal length is positive. Thus, the value of v will be positive and less than the value of u and f irrespective of the value of u. Therefore, the virtual image is formed between the principal focus point and the pole of the convex mirror. Now, m – (v/u) = – v (+ ve and < u) / u(-ve) < +1. Thus, the image will be erect and diminished. (-N.C.E.R.T. Textual Questions-UNIT 6/Optics)
(d) If an object is placed between the pole and the focus of a concave mirror, implies that u < f, and as we can write from the mirror formula, v = u f / (u – f). Since u < f, it means that v will be positive and the focal length of the concave mirror is negative, v >u. Using the relation of linear magnification, m = – (v/u) = – v (+ ve and > u) / u(-ve) > +1. The image formed in this case will be virtual, erect, and magnified
Q. 6.16. N.C.E.R.T. Textual Questions-UNIT 6/Optics
A small pin fixed on a tabletop is viewed from above, from a distance of 50 cm. By what distance would the pin appear to be raised, if it is viewed from the same point through a 15 cm thick glass slab, held parallel to the table? The refractive index of glass = 1.5. Does the answer depend on the location of the slab?
ANSWER:
In reference to the position of the pin, the normal shift is given by, d = t [1- 1/(n)] where n is the refractive index of the glass slab. The real thickness of the glass slab is given as t = 15 cm, so the normal shift will be computed as d = t [1- 1/(n)] = 15[1-1/1.5] = 15[(1.5 -1)/1.5] = 5 cm. The normal shift does not depend upon the location of the slab.
Q. 6.17. N.C.E.R.T. Textual Questions-UNIT 6/Optics
(a) Fig. 6. 03 shows a cross-section of a light pipe made of glass fibre with refractive index 1.68. The outer covering of the pipe is made of a material with a refractive index of 1.44. What is the range of the incident rays with the axis of the pipe, for which the total internal reflection inside the pipe takes place as shown in the figure? (b) What is the answer, if there is no outer covering of the pipe?
ANSWER:

(a) Given that, the relative refractive index of the glass fibre with respect to air is, ang = 1.68 and the relative refractive index of the outer coating with respect to air is, a n c = 1.44. Consider that the critical angle for the fibre material is C, then the relative refractive index of the glass fibre w.r.t the coating material will be given as c n g = 1/Sin C = ang / a n c = 1.68/1.44 = 1.167 => 1/Sin C = 1.167, thus C = 58.97o (N.C.E.R.T. Textual Questions-UNIT 6/Optics)
Let i be the angle of incidence which the light ray travelling in the air makes with the axis of the pipe and undergoes refraction at an angle r as shown in Fig. 6.03. Let us further suppose that the refracted ray is incident on the glass fibre coating interface at an angle i*. The total internal reflection will take place when i* is greater than the critical angle (C = 58.97o) for the glass fibre and coating interface. (N.C.E.R.T. Textual Questions-UNIT 6/Optics)
Therefore, r will be the maximum when i* = C. Therefore, the maximum value of r is given by, r = 90o – 58.97o = 31.03o. Now the relative refractive index of glass-fibre w.r.t air is, ang = Sin i /Sin31.03o = 1.68=> i=60o. This is the maximum value of i, which implies that all the rays having an angle of incidence between 0o to 60o will undergo total internal reflection.
(b) Let us suppose that when there is no outer covering of the pipe, then the value of the critical angle is C* so that we can write, ang = 1.68 = 1/Sin C*=> Sin C*= 1/1.68 => C* = 36.53o. For i =0o and r = 0o, we can write, i* = 90o– r = 90o– 0 =90oSince, we see that i* is greater than C*, therefore, the light ray will suffer total internal reflection when i = 0o.
The angle of refraction for i = 90o will come out as, Sin r = Sin 90/1.68 => r = 36.53o and so i* = 90 -r = 90 – 36.53 = 53.37o. We see here that i* > C*(53.37o > 36.53o), the light ray will suffer total internal reflection when i =90o. It is, therefore, concluded that all the light rays incident in the range 0o to 90o will undergo total internal reflection
Q. 6.18. N.C.E.R.T. Textual Questions-UNIT 6/Optics
Answer the following questions.
- (a) You have learned that plane and convex mirrors produce virtual images of objects. Can they produce real images under some circumstances? Explain.
- (b) A virtual image, we always say cannot be caught on the screen. Yet, when we see a virtual image, we are obviously bringing it onto the screen (therefore, the retina) of our eye. Is there a contradiction?
- (c) A diver underwater looks obliquely at a fisherman standing on the bank of a lake. Would the fisherman look taller or shorter to the diver than what he actually is?
- (d) Does the apparent depth of a tank of water change, if viewed obliquely? If so, does the apparent depth increase or decrease? (N.C.E.R.T. Textual Questions UNIT6/Optics )
- (e) The refractive index of a diamond is much greater than that of ordinary glass? Is this fact of some use to a diamond cutter? (N.C.E.R.T. Textual Questions-UNIT 6/Optics)
ANSWER:
- Yes. The plane and convex mirrors can produce real images. When the plane and convex mirrors are placed in the path of a ray of light, converging to a point, the mirrors bring the rays to focus on a screen placed in front of them. The point at which the beam converges acts as the virtual object for the mirrors, thus. the plain and convex mirrors produce real images when the object is virtual. (N.C.E.R.T. Textual Questions-UNIT 6/Optics)
- The virtual image produced by a spherical mirror, or a lens, acts as a virtual object for the eye lens, which produces a real image of the retina. Thus, this fact confirms that there is no such contradiction.(N.C.E.R.T. Textual Questions-UNIT 6/Optics)
- In figure 6.04. Shows the fisherman AB standing on the Bank of the lake. The rays of light BH and BK from the head B of the fisherman on refraction at the water-air interface, bend towards the normal at the points, H and K and appear to come from the point. B*. Therefore, to the diver, the fisherman will appear as AB*. Therefore, taller than he actually is. It may be pointed out that, as the aperture of the eye of the diver is very small, the points H and K will actually be very close to each other. Therefore, the fisherman would look taller than what he actually is. (N.C.E.R.T. Textual Questions-UNIT 6/Optics)

- It is because of the normal shifts in the position of the object due to the phenomenon of refraction. Let us consider that a point object is lying at the bottom of a water tank. Consider that point O represents the position of the object. When the Rays of light from the object fall on the interface of water and air, the rays of light get refracted away from the normal due to refraction. The point from which the refracted rays appear to come gives the apparent position of the object. As the rays appear to come from a point, I above point O, the object and hence the bottom of the tank appear to be raised. (N.C.E.R.T. Textual Questions-UNIT 6/Optics)
- The refractive index of diamonds (n= 2. 42) is much greater than that of ordinary glass (n=1.5). Since sine C = 1/n, the critical angle for the diamond is much less and is about 24o. Therefore, the light will undergo internal reflection again and again till the angle of incidence remains between 24o and 90o. For ordinary glass, due to the low value of its reflective index, such a range for the angle of incidence is quite small. Because of the much wider range of the angle of incidence available, a diamond cutter is able to cut the diamond so as to give it a large number of faces. Due to a large number of internal reflections taking place from these faces before the ray of light finally comes out, the diamond exhibits brilliance. (N.C.E.R.T. Textual Questions-UNIT 6/Optics

Thank you For your hard work over the years! For this, we give you the opportunity. https://google.com#1234567890 For more information, see the instructions. skfhjvkjsdjsrbhvbsrfhkis