NCERT Solutions chapter atoms Class12- Learn in Fun

NCERT Solutions chapter atoms Class12

It consists of the Problems with their solutions of all the chapters like atomic models, nuclear constitution, radioactivity etc.

Ques. 8.01:

Choose the correct alternative from clue given at the end of each statement. *NCERT Solutions chapter atoms Class12*

(a) The size of the atom in Thomson’s model(much greater than/ no different from/much less than)

(b) In the ground state of – – – – – – – – -, electrons are in stable equilibrium ; while in – – – – – – – -; electrons always experience a net force. (Thomson’s model / Rutherford’s model)

(c) A classical atom based on – – – – – – is deemed to collapse. (Thomson’s model /Rutherford’s model)

(d) An atom has a nearly continuous mass distribution in a – – – – – – – but has a highly non- uniform mass distribution in – – – – – – – – – – – -(Thomson’s model / Rutherford’s model)

(e) The positively charged part of the atom possesses most of the mass in – – – – – – – -(Rutherford’s model/both the model) *NCERT Solutions chapter atoms Class12*

Answer:

(a) no different from (b) Thomson’s model, Rutherford’s model (c) Rutherford’s model (d) Thomson’s model, Rutherford’s model (e) both the model

Ques. 8.02:

Suppose you are given a chance to repeat the alpha- particle scattering experiment using a thin sheet of solid hydrogen in place of the gold foil. (Hydrogen is a solid at temperature below 14 K). What results do you expect? *NCERT Solutions chapter atoms Class12*

Answer:

Hydrogen nucleus (₁H¹) having only one proton has mass = 1.67 x 10^-27 Kg and the mass of alpha particle (₂He⁴) = 6.64 x 10^-27 Kg. When the α-particles are made to incident on a thin sheet of solid hydrogen, in place of thin gold foil, the α-particles will not be scattered, even in a head on collision. The will not take place in this case because of the reason that the scattering particle is more massive than the target particle. *NCERT Solutions chapter atoms Class12*

Ques. 8.03:

What is the shortest wavelength present in the Paschen Series of spectral lines in hydrogen atom? *NCERT Solutions chapter atoms Class12*

Answer:

The wavelengths present in the Paschen Series of spectral lines in hydrogen atom are given by

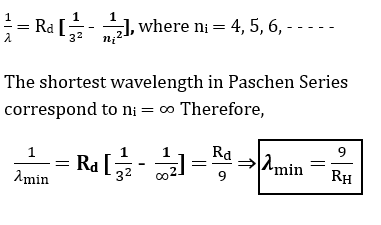
Ques. 8.04:

A difference of 2.3 eV separates to energy levels in an atom. What is the frequency of radiation emitted, when the atom makes a transition from the upper level to the lower level? *NCERT Solutions chapter atoms Class12*

Answer:

Given here, E = 2.3 eV= 2.3 x 1.6 x 10^-19 = 3.68 x 10^-19 J

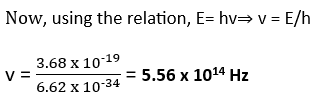
Ques. 8.05:

The ground State energy of hydrogen atom is -13.6 electron volt. What are the kinetic and potential energies of the electron in this state? *NCERT Solutions chapter atoms Class12*

Answer:

Since, the kinetic energy of the electron in an orbit is numerically equal to its total energy, therefore, the kinetic energy of the electron = 13.6 eV. The potential energy of the electron in an orbit is equal to the double of its total energy. Hence, the potential energy of the electron will be = 2 x (-13.6 eV). This implies that E_P = -27.2 eV

Ques. 8.06:

Hydrogen atom initially in the ground state absorbs a photon, which excites it to the n = 4 level. Determine the wavelength and frequency of the photon. *NCERT Solutions chapter atoms Class12*

Answer:

The ground state energy of the electron in a hydrogen atom is, E₁ = -13.6 eV and the energy of the electron in the level of energy corresponding to n= 4, in an hydrogen atom is, E₄ = -13.6 eV/ 4² ⇒E₄ = – 0.85 eV

Thus, the energy required for the   excitation of the electron from ground state to 4^th excited state will be, E = E₄ – E₁ = – 0.85 eV – (-13.6 eV) = 12.75 eV = 12.75 x 1.6 x 10^-19 J. Thus, E = hv => v = E/h = 12.75 x 1.6 x 10^-19 J/6.62 x 10^-34 J s = 3.08 x 10¹⁵ Hz and the wavelength of the exciting photon will be, 𝛌 = c/v, therefore, 𝛌 = 3 x 10⁸ m / 3.08 x 10¹⁵ Hz = 9.74 x 10^-8 m.

Ques. 8.07:

(a) Using the Bohr’s atom model, calculate the speed of the electron in a hydrogen atom in the levels, n =1, 2, and 3.

(b) Calculate the orbital period in each of these levels. *NCERT Solutions chapter atoms Class12*

Answer:

Ques. 8.08:

The radius of the innermost electron orbit of a hydrogen atom is 5.3 x 10^-11 m. What are the radii of the n = 2 and n =3 orbits. *NCERT Solutions chapter atoms Class12*

Answer:

As is clear that the radius of an orbit in H-atom is directly proportional to the square of its principal quantum number: r ∝ n². Let us consider that the radii of the orbits corresponding to n=1, 2, and 3 be r₁, r₂, and r₃, then it can be written as r₂/r₁ = 2²/1² =4 ⇒ r₂ = 4 x r₁ = 4 x 5.3 x 10^-11 = 2.12 x 10^-10 m.

r₃/r₁ = 3²/1² =9 ⇒ r₃ = 9 x r₁ = 9 x 5.3 x 10^-11 = 4.77 x 10^-10 m.

Ques. 8.09:

A 12.5 eV electron beam is used to bombard gaseous hydrogen at room temperature. What series of wavelength will be emitted? *NCERT Solutions chapter atoms Class12*

Answer:

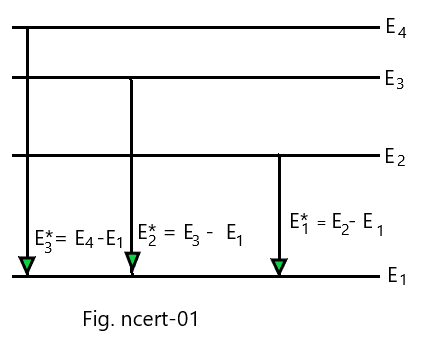
If the first, second and third excited energies for the hydrogen atom be E₁*, E₂* and E₃*, then we can write,

E₁*= E₂ – E₁ =-3.4 eV – (-13.6 eV) = 10.2 eV

E₂* = E₃ – E₁ = -1.51 eV – (-13.6 eV) = 12.09 eV

E₃*= E₄ – E₁ =-0.85 eV – (-13.6 eV) = 12.75 eV

It is clear here that the H-atoms will be raised at the most up to n = 3 level when a 12.5 eV, electron beam is made to bombard gaseous hydrogen at room temperature. The hydrogen atoms may come to ground state directly or via n=2 level. Therefore, the wavelength of the radiations emitted will lie in Balmer Series (for de-excitation from n = 3 level to n= 2 and n= 1 level) and Lyman Series (for de-excitation from n = 2 level to n= 1 level).

Ques. 8.10:

In accordance with the Bohr’s model, find the quantum number that correct characterizes the earth’s revolution around the sun in an orbit of radius 1.5 x 10¹¹ m with orbital speed 3 x 10⁴ m s^-1. (Mass of earth = 6.0 x 10²⁴ Kg. *NCERT Solutions chapter atoms Class12*

Answer:

Bohr’s model of the atom is not applicable to describe the Earth’s revolution around the Sun. Bohr’s model specifically pertains to the behavior of electrons in the atom and the quantization of their energy levels. *NCERT Solutions chapter atoms Class12*

The Earth’s motion around the Sun is governed by classical mechanics and Kepler’s laws of planetary motion. These laws describe the motion of celestial bodies under the influence of gravitational forces. The relevant parameters for characterizing the Earth’s orbit are the orbital radius, orbital speed, and mass of the Earth. *NCERT Solutions chapter atoms Class12*

The angular momentum of earth = mvr = 6.0 x 10²⁴ x 3 x 10⁴ x 1.5 x 10¹¹ = 2.7 x 10⁴⁰ Kg m s^-1

As per the postulate of Bohr’s model, mvr = nh/2π  ⇒ n = (mvr) 2π/h = 2.7 x 10⁴⁰ x 2π/6.62 x 10^-34 ≃ 10⁷⁴

Ques. 8.11:

Answer the following questions, which help you understand the difference between Thomson’s atom model and Rutherford’s atom model better. *NCERT Solutions chapter atoms Class12*

(a) Is the average angle of deflection of alpha particles by a thin gold foil predicted by Thomson’s model much less, about the same or so much greater than that predicted by Rutherford’s model. *NCERT Solutions chapter atoms Class12*

(b) Is the probability of backward scattering (i.e. scattering of alpha particles at angle greater than 90^o) predicted by Thomson’s model, much less about the same or much greater than that predicted by Rutherford’s atom model. *NCERT Solutions chapter atoms Class12*

(c) Keeping other factors fixed, it is found experimentally that for small thickness t, the number of alpha particles scattered at moderate angles, is proportional to t. What clue does this linear dependence on t provides? *NCERT Solutions chapter atoms Class12*

(d) In which model, is it completely wrong to ignore multiple scattering for the calculations of average angle of scattering of alpha particles by a thin foil? *NCERT Solutions chapter atoms Class12*

Answer:

(a) Rutherford’s model predicts that alpha particles (helium nuclei) that approach a thin gold foil would experience significant deflections when they come close to the positively charged nucleus. This is due to the concentrated positive charge and the repulsive forces between the positively charged alpha particles and the positively charged nucleus.

In contrast, Thomson’s model would predict much less deflection of alpha particles because the positive charge is distributed throughout the atom, and the presence of a concentrated positive nucleus is not accounted for.

Experimental results conducted by Rutherford and his colleagues, known as the famous Rutherford scattering experiment, confirmed that the actual deflection of alpha particles by a thin gold foil was much greater than what Thomson’s model could explain. This experiment provided strong evidence for the existence of a concentrated positive charge in the atom’s nucleus and led to the development of the modern atomic model.

Therefore, the average angle of deflection of alpha particles predicted by Thomson’s model is much less than that predicted by Rutherford’s model. *NCERT Solutions chapter atoms Class12*

(b) According to Thomson’s model of the atom, which envisions the atom as a positively charged sphere with electrons embedded within it, the probability of backward scattering (scattering at an angle greater than 90 degrees) would be expected to be much less. This is because Thomson’s model assumes that the positive charge is distributed throughout the atom, and the electrons are spread out in a relatively uniform manner.

In contrast, Rutherford’s atom model, based on the results of the Rutherford scattering experiment, proposes that the atom has a concentrated positive charge in the form of a nucleus. According to Rutherford’s model, alpha particles that approach the atom can experience close encounters with the dense positive nucleus, resulting in significant scattering at large angles, including backward scattering.

Therefore, the probability of backward scattering predicted by Thomson’s model is much less than that predicted by Rutherford’s atom model, which better accounts for the experimental observations. *NCERT Solutions chapter atoms Class12*

(c) The linear dependence of the scattered particle count on the thickness implies that each individual atom or nucleus within the target material contributes independently to the scattering process. In other words, the scattering events are additive and proportional to the number of scattering centers encountered along the path of the alpha particles.

This observation is consistent with the concept of cross-section in scattering experiments. The cross-section represents the effective area that a target presents for scattering, and it is proportional to the number of scattering centers per unit area. In the case of a thin target, where the thickness is much smaller than the dimensions of the target area, the cross-section can be approximated by the linear relationship with the thickness.

Overall, the linear dependence of the number of scattered alpha particles on the thickness of the target material suggests that the scattering process is primarily due to individual interactions with scattering centers, such as atoms or nuclei, within the material. *NCERT Solutions chapter atoms Class12*

(d) On the basis of Thomson’s atom model, the scattering angle of alpha particles due to single collision will be very small. It is because, the mass of the atom is distributed all over it. The observed average scattering angle can be explained only by considering multiple scattering. Therefore, it is wrong to ignore multiple scattering in Thomson’s atom model.

Since the mass of the atom is concentrated in the form of nucleus in the Rutherford’s atom model, therefore, most of the scattering comes through a single collision and so the multiple scattering can be ignored. *NCERT Solutions chapter atoms Class12*

Ques. 8.12:

The gravitational attraction between electron and proton in a hydrogen atom is weaker than the Coulomb Attraction by a factor of tenant power minus 14 And at alternative way of looking at this fact is to estimate the radius of the first Bohr Orbit of a hydrogen atom. If the. electron and proton were bound only by gravitational attraction. *NCERT Solutions unit-VIII physics Class12*

Answer:

Suppose that m_e and m_p are the masses of electron and the proton and when they were bound through the gravitational force only, then it can be written as

Ques. 8.13:

Obtain an expression for the frequency of radiation emitted, when a hydrogen atomic. de-excites from level n to level n – 1. For large n, show that this frequency equals the classical frequency of revolution of the electron in the orbits. *NCERT Solutions chapter atoms Class12*

Answer:

To obtain the expression for the frequency of radiation emitted when a hydrogen atom de-excites from level n to level n – 1, we can use the Rydberg formula and the Bohr model of the atom. According to the Bohr’s model, the energy levels of the hydrogen atom are given by

E_n = -13.6 eV / n²

where n is the principal quantum number representing the energy level. When an electron transitions from a higher energy level n to a lower energy level n – 1, it emits a photon with energy equal to the difference in energy between the two levels

ΔE = E_n – E_n-1 = (-13.6 eV / n²) – (-13.6 eV / (n-1)²) = (-13.6 eV / n²) + (13.6 eV / (n-1)²)

To convert this energy difference into frequency, we can use the relation E = hν, where E is the energy of the photon, h is Planck’s constant, and ν is the frequency of the radiation. Rearranging the equation, we have,

ν = (ΔE) / h = [(-13.6 eV / n²) + (13.6 eV / (n-1)²)] / h

To show that this frequency equals the classical frequency of revolution of the electron in the orbits for large n, we need to compare this expression with the classical frequency. The classical frequency of revolution of the electron in the orbits can be calculated using the equation, ν_classical = (1 / T), where T is the period of revolution of the electron.

In the Bohr model, the electron’s orbital period can be related to the angular momentum (L) using the equation, L = (nh) / (2π). Now, solving for the period T using the relation, T = (2πL) / (nh). For large n, the angular momentum L can be approximated as L ≈ nħ, where ħ is the reduced Planck’s constant (h-bar). substituting this approximation into the equation for T

T ≈ (2πnħ) / (nh) = 2πħ / h = 2πħ / h = 2π / ν­_classical. So, for large n, the classical frequency of revolution of the electron in the orbits is approximately given by, ν_classical ≈ 1 / T ≈ 1 / (2π / ν_classical) ≈ ν_classical / (2π)

Comparing this with the expression for the frequency of radiation emitted during de-excitation given by ν = [(-13.6 eV / n²) + (13.6 eV / (n-1)²)] / h

We can see that for large n, the classical frequency of revolution of the electron (ν_classical) is approximately equal to the frequency of radiation emitted (ν). Therefore, in the limit of large n, the frequency of radiation emitted during de-excitation of a hydrogen atom from level n to level n – 1 is equal to the classical frequency of revolution of the electron in the orbits. *NCERT Solutions chapter atoms Class12*

Ques. 8.14:

Classically. an electron can be in any orbit around the nucleus of an atom. Then what determines the typical atomic size? Why is an atom not c? 1000 times bigger than its typical size? The question has greatly puzzled Bohr before. he arrived at his famous model of the atom that you have learnt in the text. to simulate what he might well have done before his discovery, let us play as follows with the basic constraints of nature and see if we can get a quantity with the dimensions of length. That is, roughly equal to the noun size of an atom. 10 to the power minus 10 meter. *NCERT Solutions chapter atoms Class12*

(a) Construct a quantity with the dimensions of length from the fundamental constraints E. and E and C determine its numerical value. *NCERT Solutions chapter atoms Class12*

(b) Removal files that. the length obtained in a is many orders of magnitude smaller than the atomic dimensions for. the it involves C, but energies of atoms are mostly in non relativistic domain where C is not expected to play any role This is what may have suggested Bohr’s two discard C and look for something else to get the right atomic size now. the plagues constant H had already been made its appearance elsewhere. *NCERT Solutions chapter atoms Class12*

Bohr’s great insight lay in recognizing that HM. E and T will yield the right atomic size Construct a quantity with the dimensions of length from HM E and E and confirm that its. numerical value has indeed the correct order of magnitude. *NCERT Solutions chapter atoms Class12*

Answer:

(a) The physical quantity having the dimensions of length constructed with the help of the fundamental constants, c, e and m_e is represented by Q such that,

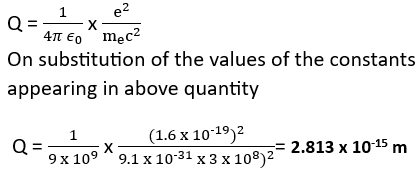
(b) The physical quantity having the dimensions of length constructed with the help of the fundamental constants, h, e and m_e is represented by the radius of the innermost orbit in the hydrogen atom which is called as Bohr radius and is given by,