What is Reflection of Light at curved surfaces?
The curved reflecting surfaces are the mirrors called concave or convex types.
Spherical Mirrors
A spherical mirror is portion of a reflecting surface which forms a part of the sphere. When we take a hollow glass sphere and a small portion of this hollow sphere is cut along a plane and silvered, then this silvered portion will attain a higher value of reflectance. This will act as a spherical mirror. Depending upon the fact that which side of the portion of the hollow glass sphere is silvered, the mirrors are of two types, namely concave mirror and convex mirror. (Reflection of Light at curved surfaces-12)
Concave Spherical Mirror
The spherical mirror is said to be a concave spherical mirror when its reflecting surface is towards the center of the sphere, of which the mirror forms a part,
As shown in the figure given here, when a portion APB is cut from the hollow glass sphere and bulging surface of this portion is silvered such that its depressed (inner) surface becomes the reflecting surface, then this portion APB is called concave spherical mirror. (Reflection of Light at curved surfaces-12)
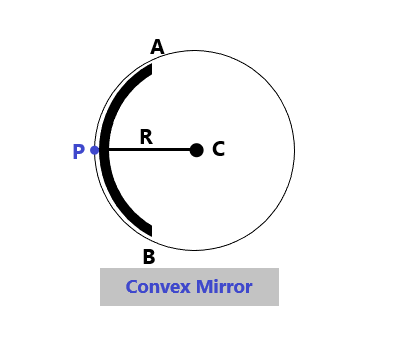
Convex spherical mirror
The spherical mirror is said to be a convex spherical mirror when its reflecting surface is away from the center of the sphere, of which the mirror forms a part,
As shown in the figure given here, when a portion APB is cut from the hollow glass sphere and depressed surface of this portion is silvered such that its bulging (outer) surface becomes the reflecting surface, then this portion APB is called convex spherical mirror. (Reflection of Light at curved surfaces-12)
Key Definitions-Reflection of Light at curved surfaces-12
- Center of Curvature: Center of curvature of the mirror is defined as the center of the sphere of which the spherical mirror forms a part. It is represented by a letter O as shown in both the figures given above.
- Radius of Curvature: Radius of curvature of a spherical mirror is defined as the radius of the sphere, of which the mirror forms a part. It is represented by R as shown in figures above where PO =R is the radius of curvature of spherical mirror ( Reflection of Light at curved surfaces)
- Pole: A pole of a spherical mirror is the center of the spherical mirror itself. In the figures given above, point P is the center of the mirror and so, it is the pole of the mirror. All the distances are measured from the pole of the mirror.
- Principal Axis of the spherical mirror: The principal axis of the spherical mirror is the line joining the pole and the center of curvature of the mirror. As shown in the figures given above, the line po extended both ways represents the principal axis of the spherical mirror. ( Reflection of Light at curved surfaces)
- Aperture of the spherical mirror: The aperture of a spherical mirror is defined as its diameter. The line joining the points A and B in the figures above represents the aperture of the spherical mirror.
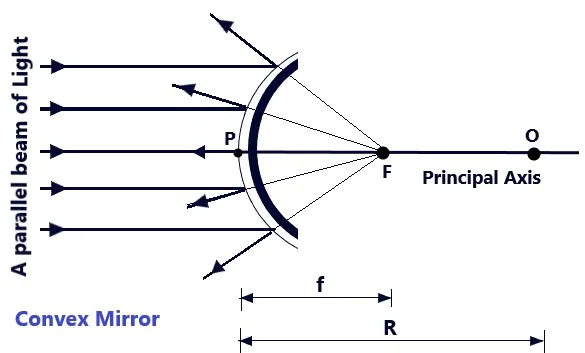
- Principal Focus: The point at which a narrow beam of light, incident on the mirror parallel to its principal axis, after reflection from the mirror converge to or appears to diverge from, is called the principal focus of the mirror. It if generally represented by F. In the case of a concave mirror, the light rays, incident parallel to the principal axis, after reflection, actually meet at the point F. On the other hand, in the case of convex mirror, the rays of light incident parallel to the principal axis after reflection from the mirror do not actually meet at the focus point F. These rays when produced backward, appear to come from the point F as shown in the figures given above.
- Focal Length: The focal length of a spherical mirror is the distance between its pole and the principal focus point. It is represented by f and as shown in the figures above, PF =f represents the focal length of the spherical mirror.
What is the relation between focal length and radius of curvature of a spherical mirror?
The focal length of a spherical mirror is equal to half of its radius of curvature, when the aperture of the spherical mirror is small, thus f = R/2. This relation between F and R is derived separately for Concave and convex spherical mirrors.
For Spherical Concave Mirror -( Reflection of Light at curved surfaces-12)
Let us consider a concave spherical mirror APB of small aperture, having P, F, and C as its pole, principal focus, and center of curvature. As shown in figure above, a ray of light parallel to its principal axis incident at point A on the mirror APB. After reflection, this ray it will pass through its principal focus F. Since OA in normal to the concave mirror at point A, so, we can proceed as under(-Reflection of Light at curved surfaces-12


For Spherical Convex Mirror– (Reflection of Light at curved surfaces-12)
Consider that a ray of light Ok is incident on a convex mirror of small aperture along a direction parallel to its principle axis at point K, as shown in the figure. The ray of light will be reflected along KG, such that it appears to come from the principal focus F of the mirror. Since CKN* is normal to the mirror at the point K, then, we can proceed as follows

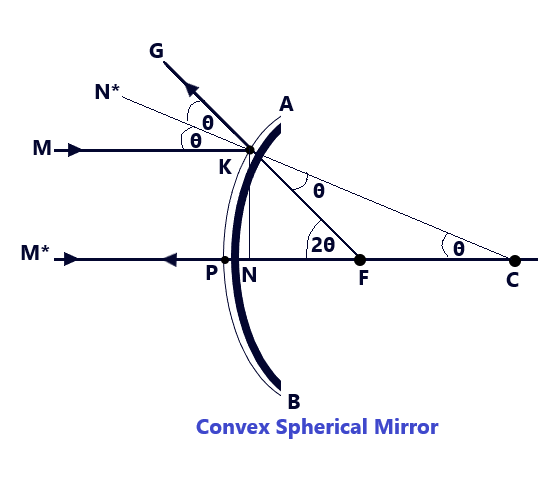
Conclusions: Taking into account the above discussions regarding the relation between the focal length and the radius of curvature of a spherical mirrors, it is found that the focal length is half of the radius of curvature in case of both, convex and concave spherical mirrors. This relation is derived on the assumption that the aperture of the spherical mirrors is considered to be small.
Conversely, if the spherical mirror is of large aperture and if a broad beam of parallel rays of light is incident on the mirror, then it is found that all the rays in the beam do not meat at (or appear to come from) a single point. This defect in spherical mirrors is called spherical aberration.


