Spherical Refracting Surfaces-12
Spherical Refracting Surfaces are the spherical refracting surfaces that form the part of a sphere of a refracting medium.
Types of Spherical Refracting surfaces-12
The Spherical Refracting Surfaces-12 are categorized into two types.
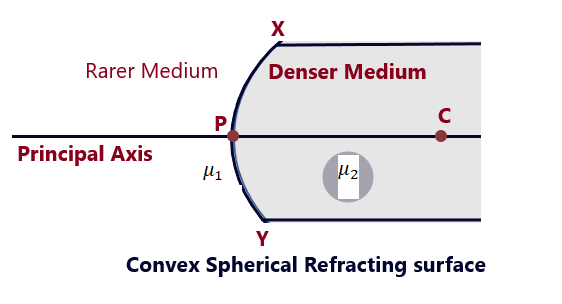
Convex Spherical Refracting Surface-12
A Spherical Refracting Surface is said to be a Convex Spherical Refracting Surface if its convex curved surface faces towards the rarer medium as shown in the fig. 01
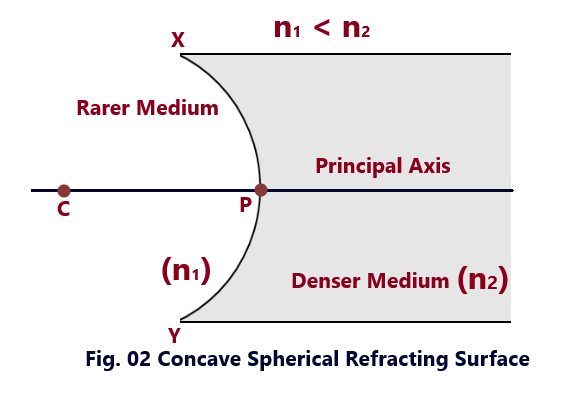
Concave Spherical Refracting Surface
A Spherical Refracting Surface is said to be a Concave Spherical Refracting Surface if its concave curved surface faces towards the rarer medium as shown in the fig. 01
What are New Cartesian Sign Conventions And Assumptions?
New Cartesian Sign Conventions: (Spherical Refracting Surface-12)
- All the distances are measured from the pole of the spherical refracting surfaces.
- The distances measured in the direction of the incident light are taken to be positive while the distances measured in the direction opposite to the direction of the incident light are taken to be negative.
Assumptions: Spherical Refracting Surface-12)
- The aperture of the spherical refracting surfaces is considered to be small.
- The object is a point object situated on the principal axis of the spherical refracting surfaces.
- The incident and the refracted rays make small angles with the principal axis of the spherical refracting surfaces.
Refraction at the convex spherical surface
Let us suppose that a point object is placed in the rarer medium at point O on the principal axis of the convex spherical refracting surface. Consider that a convex spherical refracting surface is placed in an optically rarer medium such that the convex surface is towards the rarer medium. Let. P, C, and PC =R be its pole, the center of curvature, and the radius of curvature respectively of the convex spherical refracting surface.
(a)When the object lies in the rarer medium and the image formed is real: (Spherical Refracting Surface-12
A light ray OP from the point object O incident normally on the refracting surface along the principal axis passes along the principal axis without any deviation into the denser medium.
The other light ray OA incident on the spherical refracting surface at point A, making an angle of incidence i, undergoes refraction towards the normal CAN* making an angle of refraction r. The two rays OA and OP after refraction at the convex spherical refracting surface will actually meet at the point I, on the principal axis of the convex spherical refracting surface and therefore, I is the real image of point object O. (Spherical Refracting Surface-12)
From point A, draw AK perpendicular to the principal axis of the spherical refracting surface. As per the assumptions, the aperture of the refracting surfaces is considered to be small, so point A is very close to the pole P hence, the angles alpha, beta, and gamma are also small and so they can be replaced by their tangents. (Spherical Refracting Surface-12)

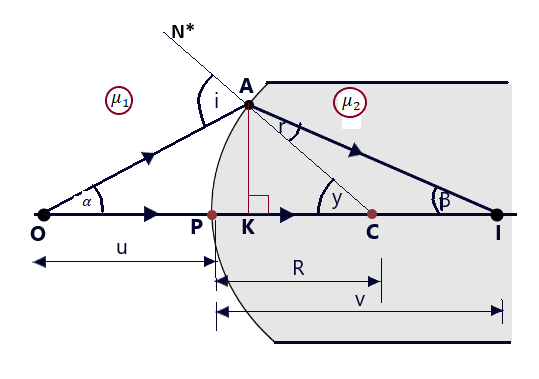
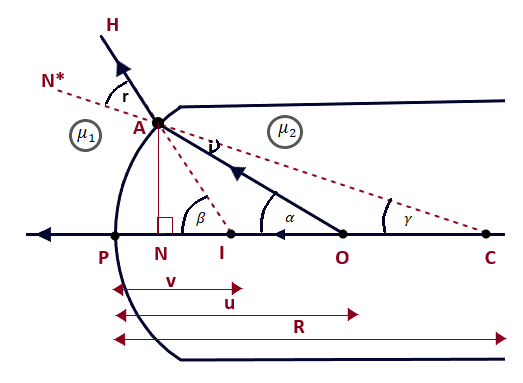
This equation (07) is the required expression which relates, the object distance (u), image distance (v) and the radius of curvature (R) of the convex refracting spherical surface. (Spherical Refracting Surface-12)
(b) When object lies in the rarer medium and image formed is virtual. When an object is situated in a rarer medium, very close to the convex spherical refracting surface, its virtual image is formed in the rarer medium.(Spherical Refracting Surface-12)
Let us suppose that a point object is placed in the rarer medium at point O on the principal axis of the convex spherical refracting surface. Consider that a convex spherical refracting surface is placed in an optically rarer medium such that the convex surface is towards the rarer medium. Let. P, C, and PC =R be its pole, the center of curvature, and the radius of curvature respectively of the convex spherical refracting surface. (Spherical Refracting Surface-12)
A light ray OP from the point object O incident normally on the refracting surface along the principal axis passes along the principal axis without any deviation into the denser medium.
The other light ray OK incident on the spherical refracting surface at point K, making an angle of incidence i, undergoes refraction (as per laws of refraction) towards the normal CAN* making an angle of refraction r. The two rays OK and OP after refraction at the convex spherical refracting surface will appear to meet at the point I, on the principal axis of the convex spherical refracting surface and therefore, I is the virtual image of point object O. (Spherical Refracting Surface-12)
From point K, draw KN perpendicular to the principal axis of the spherical refracting surface. As per the assumptions, the aperture of the refracting surfaces is considered to be small, so point N is very close to the pole P hence, the angles alpha, beta, and gamma are also small and so they can be replaced by their tangents.(Spherical Refracting Surface-12)

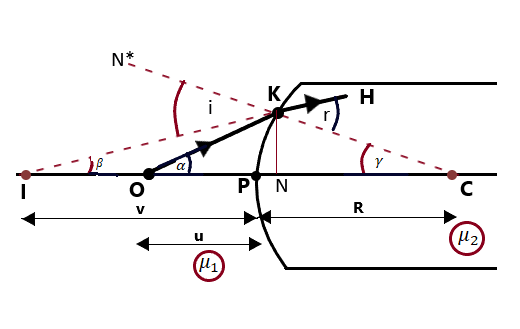
This equation (14) is the required expression which relates, to the object distance (u), image distance (v), and the radius of curvature (R) of the convex refracting spherical surface.
(c) When the object lies in the denser medium.
Let us suppose that a point object is placed in denser medium inside the convex spherical refracting surface on the principal axis at a point O. A ray of light from the object O, incident normally on the reflecting surface along the path ONP passes out into the air without any deviation.
Another ray of light OA incident at point A on the convex spherical refracting surface at an angle of incidence i, after refraction it bends away from the normal CAN* such that r is angle of refraction. The two rays appear to come from point I, on the principal axis, and therefore I is the virtual image of the point object O, formed at point L as shown in the fig. 05. . Draw a perpendicular, AN from the point A on the principal axis of the convex spherical refracting surface. From the triangle AOC, we can write,

Key points of the refraction of light ray through a convex spherical refracting surface
- When the point object (may be real or virtual) is placed on the principal axis in the rarer medium so that the incident ray travels in rarer medium and after refraction, the refracted ray, travels in denser medium, then the relation amongst,

- When the point object (may be real or virtual) is placed on the principal axis in the denser medium so that the incident ray travels in denser medium and after refraction, the refracted ray, travels in rarer medium, then the relation amongst

- The term given below is the measure of the extent to which the given convex spherical refracting surface is capable of converging or diverging the light ray when passing through it and is called the power of the spherical refracting surface.
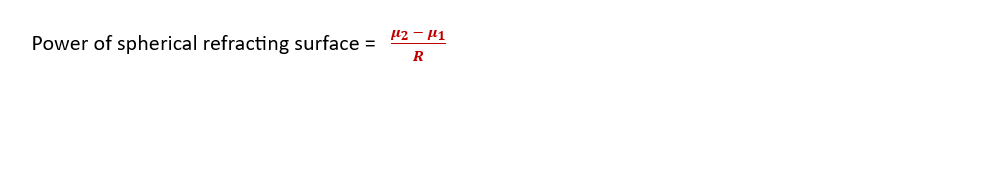
Refraction at Concave spherical surface
Let us consider a concave spherical reflecting surface is placed in an optically rarer medium. Let P, C, nd PC be the pole, the center of curvature, and the radius of curvature. Let us further consider that a point object is placed at point O in the rarer medium on the principal axis. A ray of light OP incidents normally on the concave spherical refractive surface, passes without any deviation into the denser medium.
The other ray of light. OA, incidents at the point A, at an angle of incidence i, undergoes refraction towards the normal CAN* Let r be the angle of refraction. The two rays OA and OP appear to diverge from the point I on the principal axis, and therefore I is the virtual image of the point object O as shown in the figure. Draw a perpendicular AN to principal axis of the spherical refracting surface from the point
