Lenses-12
A lens is a piece of transparent material bounded by two opposite regular spherical surfaces, either both curved or one curved, and the other plane. Such type configuration is used either singly or combined in an optical instrument for making an image by focusing the rays of light.



Lens maker’s Formula – Lenses-12
The lens maker’s formula relates the focal length of a lens to the refractive index of its material and the radii of curvature of its two surfaces that form a lens. This formula is used by the lens makers while they manufacture a lens of particular focal length from the glass of a given reflecting index. It is due to this reason that it is called the lens makers formula. The following assumptions and the new cartesian sign conventions are used while to drive the lens makers formula, (Lenses-12)
Assumptions: (Lenses-12)
- The lens is assumed to be thin so that the distances measured from the poles of the two surfaces of the lens can be taken equal to those measured from the optical center of the lens.
- The aperture of the lens is also assumed to be small.
- The object situated on the principal axis of the lens is considered to be a point of object.
- The incident ray and the refracted ray makes small angles with the principal axis of the given lens.
New Cartesian Sign Conventions: (Lenses-12)
- All the distances are measured from the optical center of the lens.
- All the distances measured in the direction of the incident ray are taken as positive and those measured in the direction opposite to the incident ray are taken as negative.
Let us consider that a biconvex lens XY bounded by two spherical refracting surfaces is placed in air having P1 and P2 as the poles, C1 and C2 as the centers of curvature and R1 and R2, the radii of curvature of two spherical refracting surfaces X P1 Y and X P2 Y of the lens respectively. Let C be the optical center of the lens as shown in the fig. 3.06. Suppose that a point object is placed at point O on the principal axis of the lens. (Lenses-12)
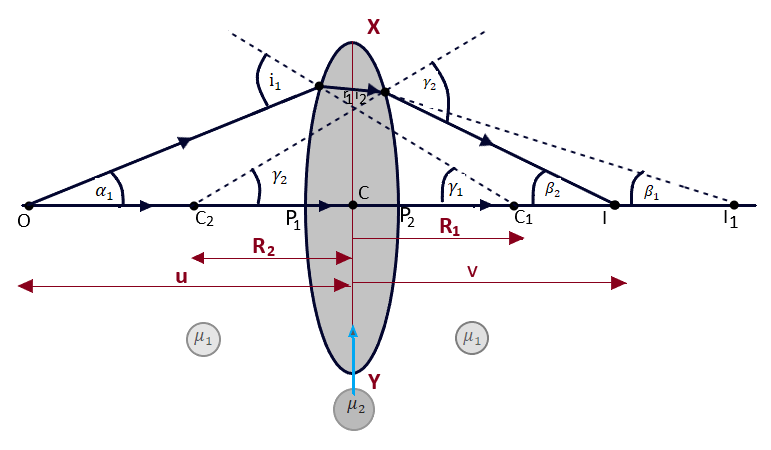
. The surface XP1 Y forms the real image I1 on the assumption that the material of the lens extends beyond the spherical surface X P1 Y as such. The following relation can be obtained from the theory of refraction through spherical surfaces.

Let us now consider the reflection from the other surface X P2 Y of the convex lens. In actual case, the material of the lens does not extend beyond the surface X P2 Y. Therefore, before the reflected ray could meet the principal axis at point I1, it will under go refraction at the second surface, XP2 Y, and the ray of light will actually come to meet the principal axis at the point of I. Thus, the real image is formed at the point I and it may be considered as the real image of the virtual object I1, placed in the material of the lens. It can be deduced that

First Principal Focus and the Focal Length (Lenses-12)
First principal focus, on the principal axis of a lens, is the position of the object for which the image is formed at infinity, as shown in Fig. 3.07 and is denoted by F1 The distance between the first principal focus and the optical center of the lens is called as first principal focal length f1 and thus, if u = C F1 = – f1, then v= infinity. Substituting these values in equation 3. 05, we get ( Lenses-12)


Second Principal Focus and the focal length (Lenses-12)
Second principal focus, on the principal axis of a lens, is the position of the image for which the object is placed at infinity, as shown in Fig. 3.08 and is denoted by F2 The distance between the second principal focus and the optical center of the lens is called as second principal focal length f2 and thus, if u = infinity, then v= C F2 = + f2. Substituting these values in equation 3. 05, we get, (Lenses-12)


Gaussian form of lens equation -Lenses-12
The lens equation or simply a lens formula is formulation, connecting the distances of the object and of image from the optical center of the lens with the focal length of the lens is called Gaussian form of lens equation or simply lens equation. This relation can directly be obtained from the lens makers formula by comparing the equations 3.05 and 3.08, we have, (Lenses-12)

This Eqn. 3.09 gives the lens equation. The lens equation and the mirror formula obtained by applying the new Cartesian sign conventions are not the same. It is to be noted that a lens forms the image on the other side of the real object, while the virtual image is formed on the same side of the object. Therefore, in case of a lens, the distance of the real image from the lens is taken as positive, and that of virtual image is taken as negative. (Lenses-12)
Derivation of Lens equation – Lenses-12
(A) For Convex Lens- When the image is real

Let us suppose that an object AB is placed at a point on the principal axis beyond F at a distance (-u). Its real image A*B* is formed on the principal axis on the other side of the lens at distance (v) from the optical center of the lens. From the Ray diagram, we see that the triangles ABC and A*B*C are similar, therefore, CA/CA* = AB/A*B* (3.10), similarly, the triangles CEF and A*B*F are also similar triangles, therefore, CF/FA* = CE/A*B*. Since CE= AB, implies that, CF/FA*= AB/A*B* (3.11). Now comparing Eqns. (3.10) and (3.11), we get, CA/CA*= CF/FA*= CF/ (CA*-CF) (3.12)
According to new cartesian sign conventions, CA= -u, CA*= +v, and CF= +f. Thus, Eqn. (3.12) can be written as -u/+v = +f/(+v -f) or – u/v = f/(v – f) or – u v + u f = v f or – v f + u f = u v Dividing both sides by u v f, we can conclude that, – 1/u + 1/v = 1/f This is the required relation between, object distance (u), image distance (v), and focal length (f) and is called lens equation
(B) For Convex Lens- When the image is virtual

Let us suppose that an object AB is placed at a point on the principal axis between F and optical center of the lens at a distance (-u) from the lens. Its virtual image A*B* an erect and large sized, is formed on the principal axis on the same side of the lens at distance (-v) from the optical center of the lens. From the Ray diagram, we see that the triangles ABC and A*B*C are similar, therefore, CA/CA* = AB/A*B* (3.13), similarly, the triangles CEF and A*B*F are also similar triangles, therefore, CF/FA* = CE/A*B*. Since CE= AB, implies that, CF/FA*= AB/A*B* (3.14). Now comparing Eqns. (3.13) and (3.14), we get, CA/CA*= CF/FA*= CF/ (CA*-CF) (3.15)
According to new cartesian sign conventions, CA= – u, CA*= – v, and CF= +f. Thus, Eqn. (3.15) can be written as – u/- v = +f/(- v + f) or u/v = f/(- v + f) or – u v + u f = v f or – v f + u f = u v. Dividing both sides by u v f, we can conclude that, – 1/u + 1/v = 1/f This is the required relation between, object distance (u), image distance (v), and focal length (f) and is called lens equation.
Derivation of lens Equation for Concave Lens-Lenses-12

Let us suppose that an object AB is placed at a point on the principal axis between F and 2F of the concave lens at a distance (-u) from the optical center of the concave lens. Its virtual image A*B* an erect and small sized, is formed on the principal axis on the same side of the concave lens at distance (-v) from the optical center of the lens. (Lenses-12)
From the Ray diagram, we see that the triangles ABC and A*B*C are similar, therefore, CA/CA* = AB/A*B* (3.16), similarly, the triangles CEF and A*B*F are also similar triangles, therefore, CF/FA* = CE/A*B*. Since CE= AB, implies that, CF/FA*= AB/A*B* (3.17). Now comparing Eqns. (3.16) and (3.17), we get, CA/CA*= CF/FA*= CF/ (CF – CA*) (3.118)- (Lenses-12)
According to new cartesian sign conventions, CA= – u, CA*= – v, and CF= – f. Thus, Eqn. (3.17) can be written as – u/- v = – f/(- f + v) or u/v = f/( f – v) or – u v + u f = v f or – v f + u f = u v. Dividing both sides by u v f, we can conclude that, – 1/u + 1/v = 1/f This is the required relation between, object distance (u), image distance (v), and focal length (f) and is called lens equation for a concave lens. (Lenses-12)
Linear Magnification in Lenses-12

The linear magnification of a lens is defined as ratio of the size of the image formed by the lens to the size of the object. It is denoted by m. When, O and I be the sizes of the object and image respectively, then, m = I/O
Let us consider that an object AB is placed on the principal axis of a convex lens of focal length f, the optical center C and its principal focus F. Then the real image A*B* of the object AB, is formed by the convex lens as shown in the figure given above. Let us further suppose that u and v are the distances of the object AB, and the image A*B*, from the optical center C of the lens. From the ray diagram, given above, we see that the triangles ABC and A*B*C are similar, therefore the ratio of their respective sides will be equal. Thus,

Applying new cartesian sign conventions, we can write AB = +O (as height of the object is upward on the principal axis), A*B* = -I (as height of the image is downward on the principal axis), CA* = + v (as the image distance is measured in the direction of incident ray), CA = – u (as the object distance is measured in the direction opposite to that of incident ray)

Summary and Key Points
- The lens maker’s formula deduced for a convex lens is applicable to both types of lenses, the convex lens and concave lens and it also relate to the power of a lens.
- The focal length of a convex lens is taken as positive, and that of a concave lens is taken to be negative.
- The radii of curvature for a convex lens R1 are positive and R2 is negative while for concave lens R1 is negative and R2 is positive.
- The lens equation and the mirror formula obtained by applying the new cartesian sign conversions are not the same. Because the lens forms the real image on the other side of the real object, while the virtual images are formed on the same side of the object. Therefore, in case of a lens, the distance of the real image from the lens is taken as positive and that of the virtual image is taken as negative.
- When a converging (convex) lens produces the real image of an object, the minimum distance required between the object and the image is equal to four times the focal length of the lens because of the reason that the lens equation gives a real solution for object distance (u) and image distance (v) only if the focal length of the lens is greater than one fourth of the distance between the object and the image.
- The linear magnification m is negative for a convex lens when it produces a real image and m will be positive when the image formed by the lens is virtual.
- The power of a lens (thick) is greater than the power of a thin lens.
Conceptive Questions and their Answers:
Q. 001: Can a convergent lens in one medium behave as a divergent lens in some other medium?
Answer: Yes. When a convex lens made of glass behaves as a convergent lens when placed in air or water. However, when the same lens is immersed in carbon disulphide, of refractive index 1.63, it behaves as a divergent lens. In other words, when a convergent lens is placed inside a transparent medium of refractive index greater than that of the material of the lens, it behaves as a divergent lens.
Q. 002: A concave mirror and a convex lens are held in water. What change, if any, do you expect in their respective focal lengths as compared to their values in air?
Answer: The focal length of a curve mirror has nothing to do with the medium in which it is placed. Hence it will remain unchanged. However, the focal length of a convex lens would change, when held in water. It increases due to the fact that the relative reflective index of the material of lens with respect to water is less than its refractive index with respect to air.
Q. 003: Why is that the sun-glasses, which have curved surfaces, do not have any power.
Answer: The two surfaces of the (goggles) lens are parallel and possess same radii of curvature. Since, one surface is convex and the other equally concave, the powers of the two surfaces is equal, but of opposite sign. The total power of the goggle lens is the algebraic sum of the powers of the individual surfaces. Therefore, P* = P1 + P2 = P + (-P) = 0.
Q. 004: Why do lenses of large aperture suffer from spherical aberration?
Answer: In case of a lens of large aperture, the behavior of the paraxial and the marginal rays are markedly different from each other. The two types of rays come to focus at different points on the principal axis of the lens. However, in case of a lens of small aperture, all the rays of light come to focus at nearly the same and a single point.
Q. 005: The image of an object formed by a lens on the screen is not in sharp focus. Suggest a method to get a clear focusing of the image on the screen without disturbing the position of the object, the lens or the screen.
Answer: The focal length of a lens depends upon the refractive index of the material of the lens, which in turn depends upon the wavelength of light. Therefore, a clear image of the object can be obtained by using light of suitable wavelength without disturbing the position of the object, the lens or the screen.
Q. 006: What is the difference between the focus and principal focus?
Answer: The point at which a parallel beam of light after the fraction through the lens comes to meet, or appears to come from, is called focus point. But the point on the principle axis at which a parallel beam of light traveling parallel to principal axis after refraction through the lens comes to meet or appears to come from is called principal focus point.
